如图1，在中，，，，另有一等腰梯形（）的底边与重合，两腰分别-优题课

如图1，在中，，，，另有一等腰梯形（）的底边与重合，两腰分别落在AB、AC上，且G、F分别是AB、AC的中点．

直接写出△AGF与△ABC的面积的比值；
操作：固定，将等腰梯形以每秒1个单位的速度沿方向向右运动，直到点与点重合时停止．设运动时间为秒，运动后的等腰梯形为（如图2）．

①探究1：在运动过程中，四边形能否是菱形？若能，请求出此时的值；若不能，请说明理由．
②探究2：设在运动过程中与等腰梯形重叠部分的面积为，求与的函数关系式．

科目数学题型解答题难度较易

知识点：圆内接四边形的性质

（1）计算： $| 1 - \sqrt{3} | + 3 \tan 30^{\circ} - {(\sqrt{3} - 5)}^{0} - {(- \frac{1}{3})}^{- 1}$ ．

（2）解不等式组 $\{\begin{matrix} 2 x + 1 > 0 ① \\ \frac{2 - x}{2} \geq \frac{x + 3}{3} ② \end{matrix}$ ．

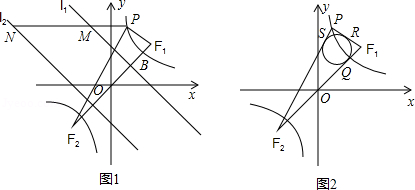
如图1所示，已知：点A（﹣2，﹣1）在双曲线 $C: y = \frac{a}{x}$ 上，直线l₁：y＝﹣x+2，直线l₂与l₁关于原点成中心对称，F₁（2，2），F₂（﹣2，﹣2）两点间的连线与曲线C在第一象限内的交点为B，P是曲线C上第一象限内异于B的一动点，过P作x轴平行线分别交l₁，l₂于M，N两点．

（1）求双曲线C及直线l₂的解析式；

（2）求证： $P F_{2} ﹣ P F_{1} ＝ MN ＝ 4$ ；

（3）如图2所示，△PF₁F₂的内切圆与F₁F₂，PF₁，PF₂三边分别相切于点Q，R，S，求证：点Q与点B重合．（参考公式：在平面坐标系中，若有点A（x₁，y₁），B（x₂，y₂），则A、B两点间的距离公式为 $AB = \sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$ .

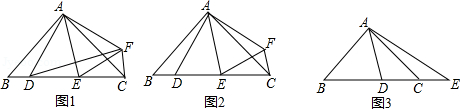
在△ABC中，AB＝AC，∠BAC＝2∠DAE＝2α．

（1）如图1，若点D关于直线AE的对称点为F，求证：△ADF∽△ABC；

（2）如图2，在（1）的条件下，若α＝45°，求证：DE²＝BD²+CE²；

（3）如图3，若α＝45°，点E在BC的延长线上，则等式DE²＝BD²+CE²还能成立吗？请说明理由．

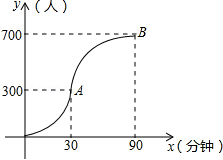
科技馆是少年儿童节假日游玩的乐园．

如图所示，图中点的横坐标x表示科技馆从8：30开门后经过的时间（分钟），纵坐标y表示到达科技馆的总人数．图中曲线对应的函数解析式为 $y = \{\begin{matrix} a x^{2}, 0 \leq x \leq 30 \\ b (^{x} + n, 30 \leq x \leq 90 \end{matrix}$ ，10：00之后来的游客较少可忽略不计．

（1）请写出图中曲线对应的函数解析式；

（2）为保证科技馆内游客的游玩质量，馆内人数不超过684人，后来的人在馆外休息区等待．从10：30开始到12：00馆内陆续有人离馆，平均每分钟离馆4人，直到馆内人数减少到624人时，馆外等待的游客可全部进入．请问馆外游客最多等待多少分钟？

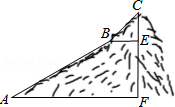
如图，为测量一座山峰CF的高度，将此山的某侧山坡划分为AB和BC两段，每一段山坡近似是“直”的，测得坡长AB＝800米，BC＝200米，坡角 $∠ BAF ＝ 30 ° ， ∠ CBE ＝ 45 °$ ．

（1）求AB段山坡的高度EF；

（2）求山峰的高度CF．（ $\sqrt{2} \approx 1.414$ ，CF结果精确到米）

试卷网试题网古诗词网作文网范文网