如图:在平面直角坐标系中A(-1,5),B(-1,0)C(-4,3).
(1)求出△ABC的面积。
(2)在下图中作出△ABC关于y轴对称图形△A1B1C1(3分)
(3)写出A1 、B1 、C1的坐标(3分)
 |
为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级: 级:非常满意; 级:满意; 级:基本满意; 级:不满意),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
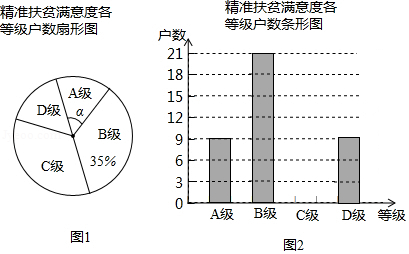
(1)本次抽样调查测试的建档立卡贫困户的总户数是 .
(2)图1中, 的度数是 ,并把图2条形统计图补充完整.
(3)某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的人数约为多少户?
(4)调查人员想从5户建档立卡贫困户(分别记为 , , , , 中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户 的概率.
如图,在四边形 中, ,点 是对角线 的中点,过点 作 的垂线,分别交 、 于点 、 ,连接 、 .试判断四边形 的形状,并证明.
先化简,再求值: ,其中 .
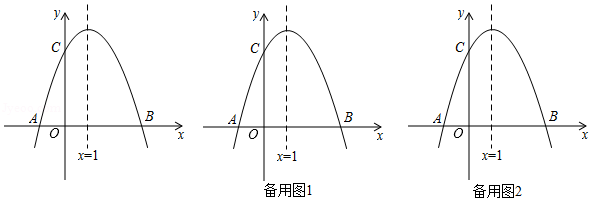
如图,已知抛物线 与 轴交于 、 两点, ,交 轴于点 ,对称轴是直线 .
(1)求抛物线的解析式及点 的坐标;
(2)连接 , 是线段 上一点, 关于直线 的对称点 正好落在 上,求点 的坐标;
(3)动点 从点 出发,以每秒2个单位长度的速度向点 运动,过 作 轴的垂线交抛物线于点 ,交线段 于点 .设运动时间为 秒.
①若 与 相似,请直接写出 的值;
② 能否为等腰三角形?若能,求出 的值;若不能,请说明理由.
"互联网 "时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为 元 为正整数),每月的销售量为 条.
(1)直接写出 与 的函数关系式;
(2)设该网店每月获得的利润为 元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?