(本题满分10分)
如图,一艘轮船由A港沿北偏东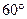 方向航行10km至B港,再沿北偏西
方向航行10km至B港,再沿北偏西 方向航行10km到达C港.
方向航行10km到达C港. (1)求A、C两港之间的距离(精确到1km)
(1)求A、C两港之间的距离(精确到1km)
(2)求点C相对于点A位置.
(11·湖州)(本小题6分)
已知:一次函数y=kx+b的图象经过M(0,2),(1,3)两点。
⑴求k,b的值;
⑵若一次函数y=kx+b的图象与x轴交点为A(a,0),求a的值。
(11·湖州)(本小题6分)因式分解:a3-9a
如图所示,过点F(0,1)的直线y=kx+b与抛物线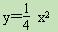 交于M(x1,
交于M(x1,
y1)和N(x2,y2)两点(其中x1<0,x2<0) .
.
(1)求b的值.
(2)求x1•x2的值
(3)分别过M、N作直线l:y=-1的垂线,垂足分别是M1、N1,判 断△M1FN1的形状,
断△M1FN1的形状,
并证明你的结论.
(4)对于过点F的任意直线MN,是否存在一条定直线m,使m与以MN为直径的圆相
切.如果有,请求出这条直线m的解析式;如果没有,请说明理由.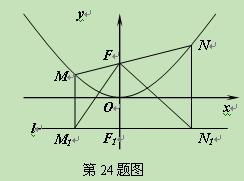
我市某镇的一种特产由于运输原因,长期只能在当地销售.当地政府对
该特产的销售投资收益为:每投入x万元,可获得利润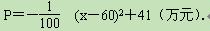
当地政府拟在“十二•五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投入100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,
可获利润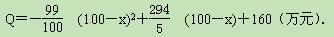
(1)若不进行开发,求5年所获利润的最大值是多少?
(2)若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?
(3)根据(1)、(2),该方案是否具有实施价值?
在圆内接四边形ABCD中,CD为∠BCA外角的平分线,F为 上
上
点,BC=AF,延长DF与BA的延长线交于E.
(1)求证△ABD为等腰三角形.
(2)求证AC•AF=DF•FE.