如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)若∠BAC = 60°,OA = 2,求阴影部分的面积(结果保留π).
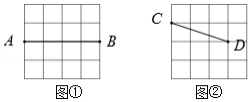
图①,图②均为 的正方形网格,每个小正方形的顶点称为格点.在图①中已画出线段 ,在图②中已画出线段 ,其中 、 、 、 均为格点,按下列要求画图:
(1)在图①中,以 为对角线画一个菱形 ,且 , 为格点;
(2)在图②中,以 为对角线画一个对边不相等的四边形 ,且 , 为格点, .
如图,在 中,点 在边 上,以 为圆心, 长为半径画弧,交边 于点 ,连接 、 .求证: .

已知 是 的反比例函数,并且当 时, .
(1)求 关于 的函数解析式;
(2)当 时,求 的值.
甲口袋中装有红色、绿色两把扇子,这两把扇子除颜色外无其他差别;乙口袋中装有红色、绿色两条手绢,这两条手绢除颜色外无其他差别.从甲口袋中随机取出一把扇子,从乙口袋中随机取出一条手绢,用画树状图或列表的方法,求取出的扇子和手绢都是红色的概率.

已知函数 为常数)
(1)当 ,
①点 在此函数图象上,求 的值;
②求此函数的最大值.
(2)已知线段 的两个端点坐标分别为 、 ,当此函数的图象与线段 只有一个交点时,直接写出 的取值范围.
(3)当此函数图象上有4个点到 轴的距离等于4,求 的取值范围.