已知：如图，O正方形ABCD的中心，BE平分∠DBC，交DC于点E，延长BC到点F，使CF＝CE，连结DF，交BE的延长线于点G，连结OG．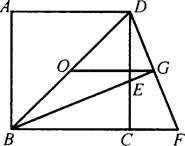
(1)说明：△BCE≌△DCF；
(2)OG与BF有什么数量关系？说明你的结论；
(3)若BC·BD＝
，求正方形ABCD的面积．
如图，⊙O的弦AB=8，直径CD⊥AB于M，OM ：MD ="3" ：2， E是劣弧CB上一点，连结CE并延长交CE的延长线于点F．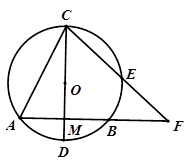
求：（1）⊙O的半径；
（2）求CE·CF的值．
“惠民”经销店为某工厂代销一种工业原料（代销是指厂家先免费提供货源，待货物售出后再进行结算，未售出的由厂家负责处理）．当每吨售价为260元时，月销售量为45吨；该经销店为提高经营利润，准备采取降价的方式进行促销，经市场调查发现：当每吨售价每下降10元时，月销售量就会增加7.5吨．综合考虑各种因素，每售出一吨工业原料共需支付厂家及其它费用100元．
（1）当每吨售价是240元时，计算此时的月销售量；
（2）若在“薄利多销、让利于民”的原则下，当每吨原料售价为多少时，该店的月利润为9000元；
（3）每吨原料售价为多少时，该店的月利润最大，求出最大利润．
如图，点E、F分别是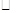
ABCD的边BC、AD上的点，且BE=DF．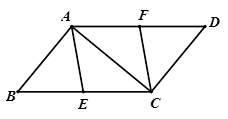
（1）求证：四边形AECF是平行四边形；
（2）若AE=BE，∠BAC＝90°，试判断四边形AECF的形状，并说明理由．
某中学开展“中国梦、我的梦”演讲比赛，甲、乙两班根据初赛成绩各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示．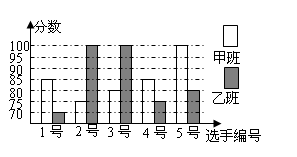
（1）根据下图，分别求出两班复赛的平均成绩和方差；
（2）根据（1）的计算结果，分析哪个班级的复赛成绩较好？
已知关于x的方程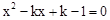
．
（1）求证：无论k取什么实数值，这个方程总有实数根；
（2）当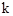
=3时，△ABC的每条边长恰好都是方程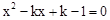的根，求△ABC的周长．