如图,点E、F分别是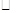 ABCD的边BC、AD上的点,且BE=DF.
ABCD的边BC、AD上的点,且BE=DF.
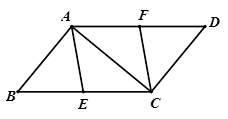
(1)求证:四边形AECF是平行四边形;
(2)若AE=BE,∠BAC=90°,试判断四边形AECF的形状,并说明理由.
(本题3分+2分)先化简,再求值: ,其中
,其中 满足x2-2x-4=0
满足x2-2x-4=0
(本题8分)2006年3月17日俄罗斯特技飞行队在名胜风景旅游区——张家界天门洞特技表演,其中一架飞机起飞后的高度变化如左下表:
| 高度变化 |
记作 |
| 上升4.5 km |
 km km |
| 下降3.2 km |
 km km |
| 上升1.1 km |
 km km |
| 下降1.4 km |
 km km |
(1)此时这架飞机比起飞点高了多少千米?
(2)如果飞机每上升或下降1千米需消耗2升燃油,那么这架飞机在这4个动作表演过程中,一共消耗了多少升燃油?
(3)如果飞机做特技表演时,有4个规定动作,起飞后高度变化如下:上升3.8千米,下降2.9千米,再上升1.6千米。若要使飞机最终比起飞点高出1千米,问第4个动作是上升还是下降,上升或下降多少千米?
(本题7分)
若|a|=5,|b|=3,(1)求a+b的值。(2)若|a+b|=a+b,求a-b的值。
(本题7分)
阅读下列内容: 请完成下面的问题:
请完成下面的问题:
如果有理数a,b满足∣ab-2∣+(1-b)2=0
试求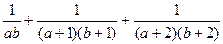 +…+
+…+ 的值
的值
(本题6分)已知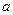 、
、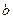 互为相反数且
互为相反数且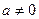 ,
,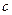 、
、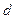 互为倒数,
互为倒数,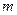 的绝对值是最小的正整数,求
的绝对值是最小的正整数,求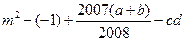 的值
的值