意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，其中从第三个数起，每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值构造如下正方形：
 |
再分别依次从左到右取2个、3个、4个、5个…正方形拼成如下长方形并记为①、②、③、④、 …相应长方形的周长如下表所示：
| 序号 |
① |
② |
③ |
④ |
… |
| 周长 |
6 |
10 |
 |
 |
… |
仔细观察图形，上表中的
，
.
若按此规律继续作长方形，则序号为⑧的长方形周长是 。
（本小题满分5分）
计算：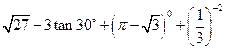
．
(10分)已知：如图，ABCD是平行四边形，P是CD上的一点，且AP和BP分别平分∠DAB和∠CBA，过点P作AD
的平行线，交AB于点Q.(1)求证：AP⊥PB；
(2)若AD=5cm，AP=8cm，求AB的长及△APB的面积.
(10分)已知：在△ABC中，AC=BC，D，E，F分别是AB，AC，CB的中点.
求证：四边形DECF是菱形.
证明题：说明理由(7分)如图，已知BE⊥
AC于E，CF⊥AB于F，BE、CF相交于点D，若BD=CD.求证：AD平分∠BAC.
证明：∵BE⊥AC于E，CF⊥AB于F
∴∠BFD=∠CED=90°
又∵∠BDF=∠CDE( ) BD=CD
∴△BDF≌△CDE( )
∴DF=DE( )
∴AD平分∠BAC( ).
解方程：(8分)
(1)2x2-4x-5=0 (2)(x-2)2=(2x+3)2