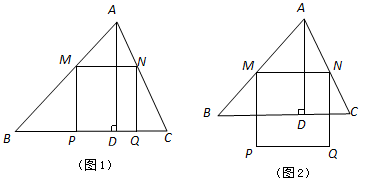
某单位欲招聘一名员工,现有 三人竞聘该职位,他们的笔试成绩和口试成绩(单位:分)分别用两种方式进行了统计,如表一和图一.
三人竞聘该职位,他们的笔试成绩和口试成绩(单位:分)分别用两种方式进行了统计,如表一和图一.
(1). 请将表一和图一中的空缺部分补充完整;
(2). 竞聘的最后一个程序是由该单位的 名职工进行投票,三位竞聘者的得票情
名职工进行投票,三位竞聘者的得票情
况如图二(没有弃权票,每名职工只能推荐一个),请计算每人的得票数;
(3). 若每票计 分,该单位将笔试、口试、得票三项测试得分按
分,该单位将笔试、口试、得票三项测试得分按 的比例确定
的比例确定
个人成绩,请计算三位竞聘者的最后成绩,并根据成绩判断谁能竞聘成功.
计算:( )(
)(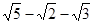 )
)
如图,点O在Rt△ABC的斜边AB上,⊙O切AC边于点E,切BC边于点D,连结OE,如果由线段CD、CE及劣弧ED围成的图形(阴影部分)面积与△AOE的面积相等,那么的值为.
一个动点在第一象限及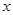 轴、
轴、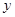 轴上运动,在第一秒钟,它从原点运动到
轴上运动,在第一秒钟,它从原点运动到 ,然后接着按图中箭头所示方向运动(即
,然后接着按图中箭头所示方向运动(即 ),且每秒移动一个单位,那么第100秒时动点所在位置的坐标是.
),且每秒移动一个单位,那么第100秒时动点所在位置的坐标是. 
已知:直线y=x+6交x轴于A点,交y轴于C两点,经过A和原点O的抛物线y==ax2+bx(a<0)的顶点B在直线AC上。
(1)求点A、C、B的坐标
(2)求出抛物线的函数关系式;
(3)以B点为圆心,以AB为半径作⊙B,将⊙B沿x轴翻折得到⊙D,试判断直线AC与⊙D的位置关系,并求出BD的长;
(4)若E为⊙B优弧 上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由
上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由
锐角△ABC中,BC=6, ,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0).
,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0).
(1) 求△ABC中边BC上高AD;
(2) 当 为何值时,PQ恰好落在边BC上(如图1);
为何值时,PQ恰好落在边BC上(如图1);
(3) 当PQ在 外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?
外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?