锐角△ABC中，BC=6，
，两动点M,N分别在边AB,AC上滑动，且MN∥BC，以MN为边向下作正方形MPQN，设其边长为x，正方形MPQN与△ABC公共部分的面积为y(y＞0)．
(1) 求△ABC中边BC上高AD；
(2) 当
为何值时，PQ恰好落在边BC上（如图1）；
(3) 当PQ在
外部时（如图2），求y关于x的函数关系式（注明x的取值范围），并求出x为何值时y最大，最大值是多少？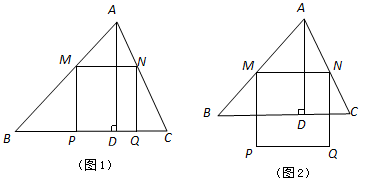
如果10b=n，那么b为n的劳格数，记为b=d（n），由定义可知：10b=n与b=d（n）所表示的b、n两个量之间的同一关系．
（1）根据劳格数的定义，填空：d（10）= ，d（10-2）= ；
（2）劳格数有如下运算性质：
若m、n为正数，则d（mn）=d（m）+d（n），d（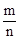
）=d（m）-d（n）．
根据运算性质，填空：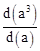
= （a为正数），若d（2）=0.3010，则d（4）= ，d（5）= ，d（0.08）= ；
（3）如表中与数x对应的劳格数d（x）有且只有两个是错误的，请找出错误的劳格数，说明理由并改正．
| x |
1.5 |
3 |
5 |
6 |
8 |
9 |
12 |
27 |
| d（x） |
 |
 |
 |
 |
 |
 |
 |
 |
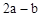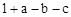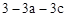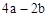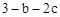如图1，在梯形ABCD中，AB∥CD，∠B=90°，AB=2，CD=1，BC=m，P为线段BC上的一动点，且和B、C不重合，连接PA，过P作PE⊥PA交CD所在直线于E．设BP=x，CE=y．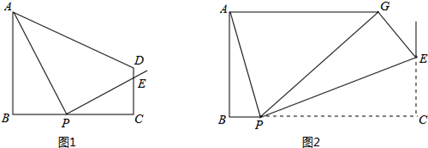
（1）求y与x的函数关系式；
（2）若点P在线段BC上运动时，点E总在线段CD上，求m的取值范围；
（3）如图2，若m=4，将△PEC沿PE翻折至△PEG位置，∠BAG=90°，求BP长．
如图，抛物线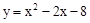
交y轴于点A，交x轴正半轴于点B．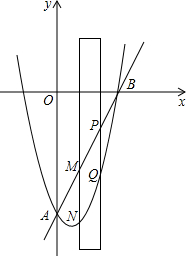
（1）求直线AB对应的函数关系式；
（2）有一宽度为1的直尺平行于x轴，在点A、B之间平行移动，直尺两长边所在直线被直线AB和抛物线截得两线段MN、PQ，设M点的横坐标为m，且0＜m＜3．试比较线段MN与PQ的大小．
如图，△ABC内接于⊙O，弦AD⊥AB交BC于点E，过点B作⊙O的切线交DA的延长线于点F，且∠ABF=∠ABC．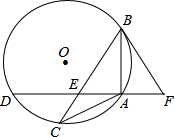
（1）求证：AB=AC；
（2）若AD=4，cos∠ABF=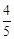
，求DE的长．
某校九（1）、九（2）两班的班长交流了为四川安雅地震灾区捐款的情况：
（Ⅰ）九（1）班班长说：“我们班捐款总数为1200元，我们班人数比你们班多8人．”
（Ⅱ）九（2）班班长说：“我们班捐款总数也为1200元，我们班人均捐款比你们班人均捐款多20%．”
请根据两个班长的对话，求这两个班级每班的人均捐款数．