如图1,在梯形ABCD中,AB∥CD,∠B=90°,AB=2,CD=1,BC=m,P为线段BC上的一动点,且和B、C不重合,连接PA,过P作PE⊥PA交CD所在直线于E.设BP=x,CE=y.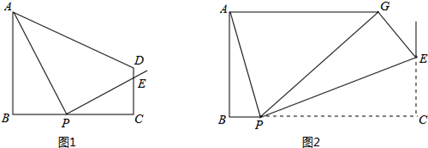
(1)求y与x的函数关系式;
(2)若点P在线段BC上运动时,点E总在线段CD上,求m的取值范围;
(3)如图2,若m=4,将△PEC沿PE翻折至△PEG位置,∠BAG=90°,求BP长.
如图,在由边长为1个单位长度的小正方形组成的 网格中,已知点 , , 均为网格线的交点.
(1)在给定的网格中,以点 为位似中心,将线段 放大为原来的2倍,得到线段 (点 , 的对应点分别为 , ,画出线段 ;
(2)将线段 绕点 逆时针旋转 得到线段 ,画出线段 ;
(3)以 , , , 为顶点的四边形 的面积是 个平方单位.

《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽,问:城中家几何?
大意:今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完,问:城中有多少户人家?
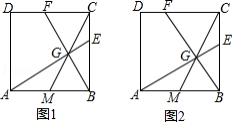
已知正方形 ,点 为边 的中点.
(1)如图1,点 为线段 上的一点,且 ,延长 、 分别与边 、 交于点 、 .
①求证: ;
②求证: .
(2)如图2,在边 上取一点 ,满足 ,连接 交 于点 ,连接 并延长交 于点 ,求 的值.
某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量 (千克)与每千克售价 (元 满足一次函数关系,部分数据如下表:
|
售价 (元 千克) |
50 |
60 |
70 |
|
销售量 (千克) |
100 |
80 |
60 |
(1)求 与 之间的函数表达式;
(2)设商品每天的总利润为 (元 ,求 与 之间的函数表达式(利润 收入 成本);
(3)试说明(2)中总利润 随售价 的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7
乙:5,7,8,7,8,9,7,9,10,10
丙:7,6,8,5,4,7,6,3,9,5
(1)根据以上数据完成下表:
|
平均数 |
中位数 |
方差 |
|
|
甲 |
8 |
8 |
|
|
乙 |
8 |
8 |
2.2 |
|
丙 |
6 |
|
3 |
(2)根据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定,求甲、乙相邻出场的概率.