如图,在平面直角坐标系xOy中,四边形ABCD是菱形,顶点A、C、D均在坐标轴上,且AB=5,sinB=
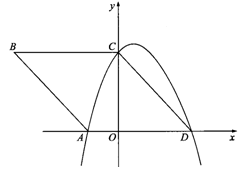
(1)求过A、C、D三点的抛物线的解析式;
(2)记直线AB的解析式为y1=mx+n,(1)中抛物线的解析式为y2=ax2+bx+c,求当y1<y2时,自变量x的取值范围;
(3)设直线AB与(1)中抛物线的另一个交点为E,P点为抛物线上A、E两点之间的一个动点,当P点在何处时,△PAE的面积最大?并求出面积的最大值.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=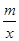 (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2. 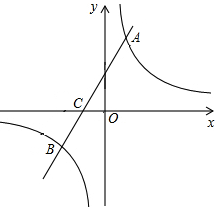
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)在x轴上求点E,使△ACE为直角三角形.(直接写出点E的坐标)
在Rt△ABC中,∠ACB=90°,D是边AB的中点,BM⊥CD于点M,已知AC=6,tanA=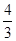 .
. 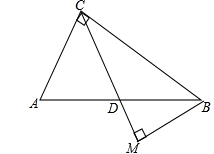
(1)求线段CD的长;
(2)求sin∠BDM的值.
某工厂原计划生产24000台空气净化器,由于雾霾天气的影响,空气净化器的需求量呈上升趋势,生产任务的数量增加了12000台.工厂在实际生产中,提高了生产效率,每天比原计划多生产100台,实际完成生产任务的天数是原计划天数的1.2倍.求原计划每天生产多少台空气净化器.
忻州有“秀容古城”之称,某校就同学们对“忻州历史文化”的了解程度进行随机抽样调查,将调查结果绘制成如下两幅统计图:
据统计图的信息,解答下列问题:
(1)本次共凋查名学生,条形统计图中m=;
(2)若该校共有学生1000名,则该校约名学生不了解有 “忻州历史文化”;
(3)调查结果中,该校八年级(2)班学生中了解程度为“很了解”的同学是两名男生、一名女生,现准备从其中随机抽取两人去市里参加“忻州历史文化”知识竞赛,用树状图或列表法,求恰好抽中一男生一女生的概率.