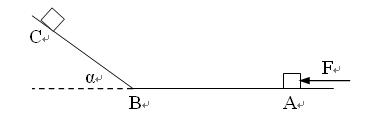
如图所示,在动摩擦因数μ=0.2的水平面AB上,水平恒力F (F大小未知)推动质量为m=1kg的物体从A点由静止开始作匀加速直线运动,物体到达B点时撤去F,接着又冲上光滑斜面(设经过B点前后速度大小不变),最高能到达C点。用速度传感器测量物体的瞬时速度,并在表格中记录了部分测量数据(g取10m/s2)。
| t/s |
0.0 |
0.2 |
0.4 |
… |
2.2 |
2.4 |
2.6 |
… |
| v/(m/s) |
0.0 |
0.4 |
0.8 |
… |
3.0 |
2.0 |
1.0 |
… |
求出物体到达B点时的速度和时间;
若撤去推力F,在A处给物体一个水平向左的初速度v0,恰能使物体运动到C点,求此初速度v0的大小。
如图,为修建高层建筑常用的塔式起重机.在起重机将质量m=5×104 kg的重物竖直吊起的过程中,重物由静止开始向上做匀加速直线运动,加速度a=0.2 m/s2,当起重机输出功率达到其允许的最大值时,保持该功率直到重物做vm=1.02 m/s的匀速运动.取g=10 m/s2,不计额外功.求:
(1)起重机允许输出的最大功率.
(2)重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率.
如图所示,一小球自平台上水平抛出,恰好无碰撞的落在临近平台的一倾角为 α = 53°的光滑斜面顶端,并刚好沿光滑斜面下滑,已知斜面顶端与平台的高度差h=0.8m,g = 10m/s2,sin53°= 0.8,cos53°= 0.6,则 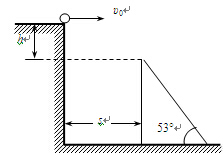
(1)小球水平抛出的初速度v0是多少?
(2)斜面顶端与平台边缘的水平距离s是多少?
(3)若斜面顶端高H = 20.8m,则小球离开平台后经多长时间t到达斜面底端
已知一颗人造卫星在半径为R的某行星上空绕该行星做匀速圆周运动,经过时间t,卫星运动的弧长为s,卫星与行星的中心连线扫过的角度是θ弧度。(已知万有引力常量为G)求:
(1)人造卫星距该行量表面的高度h;
(2)该行量的质量M;
(3)该行量的第一宇宙速度v1。
如图所示,小球在外力作用下,由静止开始从A点出发做匀加速直线运动,到B点时撤去外力.然后,小球冲上竖直平面内半径为R的光滑半圆环,恰能通过圆轨道最高点C,到达最高点C后水平抛出,最后落回到原来的出发点A处。试求:
(1)小球运动到C点时的速度;
(2)A、B之间的距离。
如图所示,有一条渡船正在渡河,河宽为400m,渡船在静水中的速度是v1=4m/s,水的流速是v2=3m/s,怎样开船过河所用时间最短?最短时间为多少?所行驶的位移为多大?