已知

(1)当 时,求
时,求 ;
;
(2) 若
 ,求实数
,求实数 的取值范围.
的取值范围.
有如下结论:“圆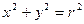 上一点
上一点 处的切线方程为
处的切线方程为 ”,类比也有结论:“椭圆
”,类比也有结论:“椭圆 处的切线方程为
处的切线方程为 ”,过椭圆C:
”,过椭圆C: 的右准线l上任意一点M引椭圆C的两条切线,切点为 A、B.
的右准线l上任意一点M引椭圆C的两条切线,切点为 A、B.
(1)求证:直线AB恒过一定点;
(2)当点M的纵坐标为1时,求△ABM的面积.
设函数 (其中
(其中 )的图象在
)的图象在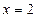 处的切线与直线
处的切线与直线 平行.
平行.
(1)求 的值;
的值;
(2)求函数 在区间[0,1]的最小值;
在区间[0,1]的最小值;
(3)若 ,
,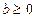 ,
, ,且
,且 ,试根据上述(1)、(2)的结论证明:
,试根据上述(1)、(2)的结论证明: .
.
已知各项均为正数的数列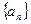 满足:
满足: ,且
,且 .
.
(1)求证:数列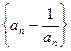 是等比数列;
是等比数列;
(2)设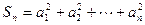 ,
,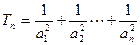 ,求
,求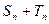 ,并确定最小的正整数n,使
,并确定最小的正整数n,使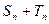 为整数.
为整数.
一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数:f1(x)=x,f2(x)=x2,f3(x)=x3,f4(x)=sinx,f5(x)=cosx,f6(x)=2.
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求恰好抽取了3次卡片的概率.
如图,在组合体中, 是一个长方体,
是一个长方体, 是一个四棱锥.
是一个四棱锥. ,
, ,点
,点 且
且 .
.
(Ⅰ)证明: ;
;
(Ⅱ)求面 与面
与面 所成的角的正切值;
所成的角的正切值;
(Ⅲ)若 ,当
,当 为何值时,
为何值时, .
.