在如图所示的空间区域里,y轴左方有一匀强电场,场强方向跟y轴正方向成60°,大小为E=4.0×105N/C;y轴右方有一垂直纸面向里的匀强磁场,磁感应强度B=0.20T。有一质子以速度v=2.0×106m/s,由x轴上的A点(10cm,0)沿与x轴正方向成30°斜向上射入磁场,在磁场中运动一段时间后射入电场,后又回到磁场,经磁场作用后又射入电场。已知质子质量近似为m=1.6×10-27kg,电荷q=1.6×10-19C,质子重力不计。求:(计算结果保留3位有效数字)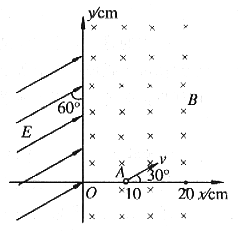
质子在磁场中做圆周运动的半径。
质子从开始运动到第二次到达y轴所经历的时间。
质子第三次到达y轴的位置坐标。
如图a所示,质量m=2.0kg的物体静止在水平面上,物体与水平面间的动摩擦因数μ=0.2。从t=0时刻起,物体受到一个水平力F的作用而开始运动,前8s内F随时间t变化的规律如图b所示,g取10m/s2。求:
前8s内物体的位移;
在图c的坐标系中画出物体在前8s内的v-t图象。
如图所示,一个人用与水平方向成θ=30°角的斜向下的推力F推一个重G=200N的箱子匀速前进,箱子与地面间的动摩擦因数为μ=0.4,g取10m/s2。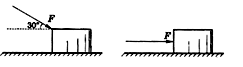
求推力F的大小;
若人不改变推力F的大小,只把力的方向变为水平去推这个静止的箱子,推力作用时间t=3s后撤去,求撤去推力F后箱子还能滑行多远停下来?
为了安全,公路上行驶的汽车间应保持必要的距离。某市规定,车辆在市区内行驶的速度不得超过40km/h。有一辆车发现前面25m处发生交通事故紧急刹车,紧急刹车产生的最大加速度为5m/s2,反应时间为t=0.5s。经测量,路面刹车痕迹为S=14.4m。求:该汽车是否违章驾驶?
是否会有安全问题?
如右图所示,水平放置的平行板电容器,与某一电源相连,它的极板长L=0.4 m,两板间距离d=4×10-3 m,有一束由相同带电微粒组成的粒子流,以相同的速度v0从两板中央平行极板射入,开关S闭合前,两板不带电,由于重力作用微粒能落到下板的正中央,已知微粒质量为m=4×10-5 kg,电量q=+1×10-8 C.(g=10 m/s2)求:微粒入射速度v0为多少?
为使微粒能从平行板电容器的右边射出电场且不接触平行板,电容器的上板应与电源的正极还是负极相连?所加的电压U应取什么范围?

如图所示,电源电动势为E=30V,内阻为r=1Ω,电灯上标有“6V、12W”字样,直流电动机线圈电阻R=2Ω。若电灯恰能正常发光,求电动机输出的机械功率。