(本题3分+3分+4分)如图,已知二次函数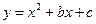 的图象与x轴交于A、B两点,与y轴交于点P,顶点为C(
的图象与x轴交于A、B两点,与y轴交于点P,顶点为C(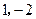 )。
)。
(1)求此函数的关系式;
(2)作点C关于x轴的对称点D,顺次连接A、C、B、D.若在抛物线上存在点E,使直线PE将四边形ACBD分成面积相等的两个四边形,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点F,使得△PEF是以P为直角顶点的直角三角形?若存在,求出点F的坐标;若不存在,请说明理由。
某班到毕业时共结余班费1800元,班委会决定拿出不少于270元但不超过300元的资金为老师购买纪念品,其余资金用于在毕业晚会上给50位同学每人购买一件T恤或一本影集作为纪念品.已知每件T恤比每本影集贵9元,用200元恰好可以买到2件T恤和5本影集.
⑴求每件T恤和每本影集的价格分别为多少元?
⑵有几种购买T恤和影集的方案?
如图,已知反比例函数 的图像经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数
的图像经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数 的图象上另一点C(n,一2).
的图象上另一点C(n,一2).
⑴求直线y=ax+b的解析式;
⑵设直线 y=ax+b与x轴交于点M,求AM的长.
y=ax+b与x轴交于点M,求AM的长.
有A、B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B布袋中有三个完全相同的小球,分别标有数字-l,-2和-3.小强从A布袋中随机取出一个小球,记录其标有的数字为a,再从B布袋中随机取出一个小球,记录其标有的数字为b,这样就确定点Q的一个坐标为(a,b).
⑴用列表或画树状图的方法写出点Q的所有可能坐标;
⑵求点Q落在直线y=x-3上的概率.
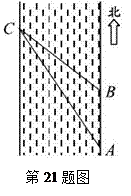
一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C, 测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这条河的宽度.(参考数值:tan31°≈
测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这条河的宽度.(参考数值:tan31°≈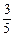 )
)
先化简,再求值: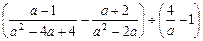 ,其中a=2-
,其中a=2-