(本题8分)已知关于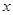 的方程
的方程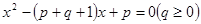 的两实根为
的两实根为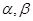 ,且
,且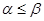 .
.
⑴试用含有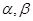 的代数式表示
的代数式表示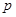 和
和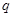 ;
;
⑵求证: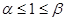 ;
;
⑶若以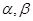 为坐标的点
为坐标的点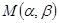 在△ABC的三边上运动,且△ABC顶点的坐标分别为A
在△ABC的三边上运动,且△ABC顶点的坐标分别为A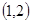 ,B
,B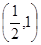 ,C
,C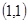 ,问是否存在点M,使
,问是否存在点M,使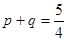 ,若存在,求出点M的坐标;若不存在,请说明理由.
,若存在,求出点M的坐标;若不存在,请说明理由.
如图正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABO的三个顶点A,B,O都在格点上.画出△ABO绕点O逆时针旋转90°后得到的三角形
已知一元二次方程ax2+bx+c=0(a≠0)中的两根为 请你计算x1+x2=____________, x1·x2=____________.
请你计算x1+x2=____________, x1·x2=____________.
并由此结论解决下面的问题:
(1)方程2x2+3x-5=0的两根之和为______,两根之积为______.
(2)方程2x2+mx+n=0的两根之和为4,两根之积为-3,则m=______,n=______.
(3)若方程x2-4x+3k=0的一个根为2,则另一根为______.
(4)已知x1,x2是方程3x2-2x-2=0的两根,不解方程,用根与系数的关系计算代数式 的值.
的值.
如图,菱形ABCD中,AC,BD交于O,AC=8m,BD=6m,动点M从A出发沿AC方向以2m/s匀速直线运动到C,动点N从B出发沿BD方向以1m/s匀速直线运动到D,若M,N同时出发,问出发后几秒钟时,ΔMON的面积为

二次函数y=ax2+bx+c(a≠0)的图象如图所示,求:
(1)对称轴是____________;
(2)函数解析式____________;
(3)当x______时,y随x增大而减小;
(4)由图象回答:
当y>0时,x的取值范围______;
当y=0时,x=______;
当y<0时,x的取值范围_____.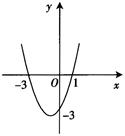
关于x的方程x2-2x+k-1=0有两个不等的实数根.
(1)求k的取值范围;
(2)若k+1是方程x2-2x+k-1=4的一个解,求k的值.