在抗洪抢险中，人民解放军的冲锋舟沿东西方向的河流抢救灾民，早晨从A地出发，晚上到达B地，约定向东为正方向，当天的航行路程记录如下（单位：千米）：14，−9，+8，−7，13，−6，+10，−5．
（1）B地在A地何处？
（2）若冲锋舟每千米耗油0.5升，油箱容量为29升，求途中还需补充多少升油？
大家已经知道，完全平方公式和平方差公式可以用平面几何图形的面积来表示，实际上还有一些代数恒等式也可以用这种形式表示，例如：2x（x+y）=2x2+2xy就可以用图的面积表示．
（1）请写出图（2）所表示的代数恒等式： _______ ；
（2）请写出图（3）所表示的代数恒等式： ________ ；
（3）试画出一个几何图形，使它的面积能表示（x+y）（x+3y）=x2+4xy+3y2．
（1）比较左、右两图的阴影部分面积，可以得到乘法公式 _________ （用式子表达）．
（2）运用你所得到的公式，计算（a+2b﹣c）（a﹣2b﹣c）．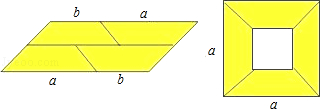
如图，边长为a的大正方形内有一个边长为b的小正方形．
（1）阴影部分面积是 _________ ．
（2）小欣把阴影部分的两个四边形拼成如图所示的长方形，则这个长方形的宽是 _______ 面积是 _______ ．
（3）由此可验证出的结论是 _________ ．
计算6（7+1）（72+1）（74+1）（78+1）+1的值
试判断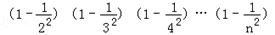
的值与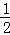
的大小关系，并证明你的结论．