简答题(共2题,每小题3分,共6分)
(1)根据生活经验,对代数式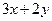 作出解释.
作出解释.
(2) 两个有理数的和是负数,那么这两个数一定都是负数,这种说法对吗?如果不对,请举例说明?
如图,AC切⊙O于点C,AB过圆心O交⊙O于点B、D,且AC=BC,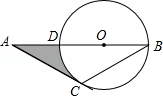
(1)求∠A的度数;
(2)若⊙O的半径为2,求图中阴影部分的面积.
如图,点A、B、C、D在⊙O上,AB与OC、OD分别相交于点E、F,如果AE=BF,那么AC与BD相等吗?请说明理由.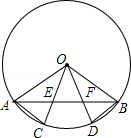
已知关于x的一元二次方程x2+mx+n+1=0的一根为2.
(1)求n关于m的关系式;
(2)试说明:关于y的一元二次方程y2+my+n=0总有两个不相等的实数根.
解方程:
(1)2x2﹣5x﹣1="0"
(2)(2x+3)2=﹣6x﹣3.
如图,已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=8,CD=10.
(1)求梯形ABCD的面积;
(2)动点P从点B出发,以2个单位/s的速度沿B→A→D→C方向向点C运动;动点Q从点C出发,以2个单位/s的速度沿C→D→A方向向点A运动;过点Q作QF⊥BC于点F.若P、Q两点同时出发,当其中一点到达终点时另一点也随之停止运动,设运动时间为t秒.问:
①当点P在B→A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值,并判断此时PQ是否平分梯形ABCD的面积;若不存在,请说明理由.
②在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.