（本题10分） 随着大陆惠及台胞政策措施的落实，台湾水果进入了大陆市场。一水果经销商购进了A，B两种台湾水果各10箱，分配给他的甲、乙两个零售店（分别简称甲店、乙店）销售。预计每箱水果的盈利情况如下表：
| |
A种水果/箱 |
B种水果/箱 |
| 甲店 |
11元 |
17元 |
| 乙店 |
9元 |
13元 |
有两种配货方案（整箱配货）：
方案一：甲、乙两店各配货10箱，其中A种水果两店各5箱，B种水果两店各5箱；
方案二：按照甲、乙两店盈利相同配货，其中A种水果甲店_________箱，乙店__________箱；B种水果甲店_________箱，乙店__________箱.
（1） 如果按照方案一配货，请你计算出经销商能盈利多少元？
（2） 请你将方案二填写完整（只填写一种情况即可），并根据你填写的方案二与方案一作比较，哪种方案盈利较多？
（3） 在甲、乙两店各配货10箱，且保证乙店盈利不小于100元的条件下，请你设计出使水果经销商盈利最大的配货方案，并求出最大盈利为多少？
解方程：
（1）x2-4x=0
（2）2x2+5x+1=0．
（3）x2-6x+9=（5-2x）2
（4）
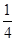x2-x-4=0（用配方法）
（本题12分）已知，如图，在平面直角坐标系中，点A、B的横坐标恰好是方程
的解，点C的纵坐标恰好是方程
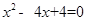的解，点P从C点出发沿y轴正方向以1个单位/秒的速度向上运动，连PA、PB，D为AC的中点.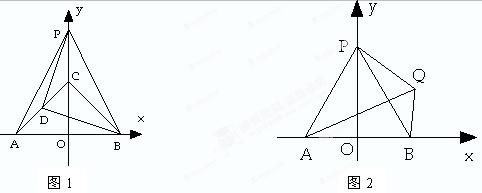
1）求直线BC的解析式；
2）设点P运动的时间为t秒，问：当t为何值时，DP与DB垂直且相等？
3）如图2，若PA=AB，在第一象限内有一动点Q，连QA、QB、QP，且∠PQA=60°，问：当Q在第一象限内运动时，∠APQ+∠ABQ的度数和是否会发生改变？若不变，请说明理由并求其值.
（本题10分）如图，正方形ABCD和正方形AEFG有公共的顶点A，连BG、DE，M为DE的中点，连AM.
（1）如图1，AE、AG分别与AB、AD重合时，AM和BG的大小和位置关系分别是、_ ____；
（2）将图1中的正方形AEFG绕A点旋转到如图2，则（1）中的结论是否仍成立？试证明你的结论；
（3）若将图1中的正方形AEFG绕A点逆时针旋转到正方形ABCD外时，则AM和BG的大小和位置关系分别是__________、____________，请你在图3中画出图形，并直接写出结论，不要求证明.
（本题10分）如图，利用一面墙（墙的长度为20m），用34m长的篱笆围成两个鸡场，中间用一道篱笆隔开，每个鸡场均留一道1m宽的门，设AB的长为x米.
（1）若两个鸡场总面积为96m2，求x；
（2）若两个鸡场的面积和为S，求S关于x的关系式；
（3）两个鸡场面积和S有最大值吗？若有，最大值是多少？
（本题8分）P是边长为4的正方形ABCD的边BC上任意一点，过B点作BG⊥AP于G，过C点作CE⊥AP于E，连BE.
（1）如图1，若P是BC的中点，求CE的长；
（2）如图2，当P在BC边上运动时，（不与B、C重合）求(AG-CE)/BE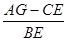
的值；