（本题12分）已知，如图，在平面直角坐标系中，点A、B的横坐标恰好是方程
的解，点C的纵坐标恰好是方程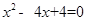
的解，点P从C点出发沿y轴正方向以1个单位/秒的速度向上运动，连PA、PB，D为AC的中点.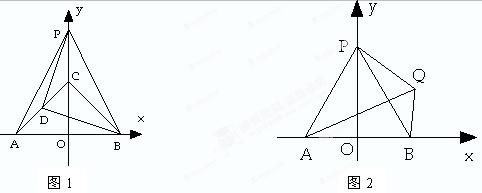
1）求直线BC的解析式；
2）设点P运动的时间为t秒，问：当t为何值时，DP与DB垂直且相等？
3）如图2，若PA=AB，在第一象限内有一动点Q，连QA、QB、QP，且∠PQA=60°，问：当Q在第一象限内运动时，∠APQ+∠ABQ的度数和是否会发生改变？若不变，请说明理由并求其值.
已知，如图，在□ABCD中，∠BAD和∠BCD的平分线AF，CE分别与对角线BD交于点F，E．求证：四边形AFCE是平行四边形．
如图，已知在△ABC中，AB=AC，AB的垂直平分线DE交AC于点E，CE的垂直平分线正好经过点B，与AC相交于点F，求∠A的度数．
为了提高产品的附加值，某公司计划将研发生产的1200件新产品进行精加工后再投放市场．现有甲、乙两个工厂都具备加工能力，公司派出相关人员分别到这两间工厂了解情况，获得如下信息：
信息一：甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天；
信息二：乙工厂每天加工的数量是甲工厂每天加工数量的1．5倍．
根据以上信息，求甲、乙两个工厂每天分别能加工多少件新产品？
如图，在□ABCD中，点E是DC的中点，连接AE，并延长交BC的延长线于点F．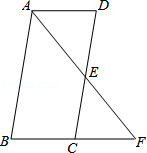
（1）求证：△ADE和△CEF的面积相等；
（2）若AB=2AD，试说明AF恰好是∠BAD的平分线．
（1）化简：
+
．
（2）解分式方程：