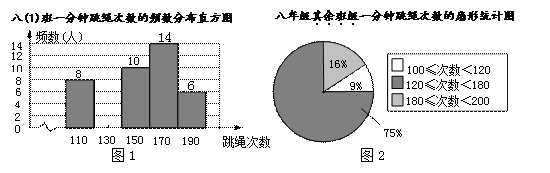
(本题12分)某校积极开展每天锻炼1小时活动,老师对本校八年级学生进行一分钟跳绳测试,并对跳绳次数进行统计,绘制了八(1)班一分钟跳绳次数的频数分布直方图和八年级其余班级一分钟跳绳次数的扇形统计图.已知在图1中,组中值为190次一组的频率为0.12.(说明: 组中值为190次的组别为 180≤次数<200)
 |
请结合统计图完成下列问题:
(1)八(1)班的人数是 ,组中值为110次一组的频率为 ;
(2)请把频数分布直方图补充完整;
(3)如果一分钟跳绳次数不低于120次的同学视为达标,八年级同学一分钟跳绳的达标率不低于90%,那么八年级同学至少有多少人?
某支股票上周末的收盘价格是10.00元,李先生买了2000股,本周一到周五的这支股票的收盘情况如下表:(“+”表示股票比前一天上涨,“-”表示股票比前一天下跌)
| 上周末收盘价 |
周一 |
周二 |
周三 |
周四 |
周五 |
| 10.00 |
+0.28 |
-0.36 |
+0.38 |
-0.35 |
+0.25 |
(1)周三这支股票的收盘价是多少元?
(2)本周末的收盘价与上周末收盘价相比是怎样变化的?
(3)李先生在本周五将股票全部卖出,若不考虑其他因素,请分析李先生在本次股票买卖过程中的盈亏情况.
先化简求值
 ,其中a=-1,b=
,其中a=-1,b= .
.
(本题满分16分,每题4分)
(1)计算:
(2)计算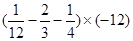
(3)解方程:
(4)解方程:
用圆规、直尺作图,不写作法,但要保留作图痕迹.
如图,已知线段m,n,求作线段AB,使AB=2m+n;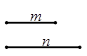
如图,直线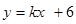 与x轴y轴分别相交于点E,F.点E的坐标(8,0),点A的坐标为(6,0)。点P(x,y)是第一象限内的直线上的一个动点(点P不与点E,F重合).
与x轴y轴分别相交于点E,F.点E的坐标(8,0),点A的坐标为(6,0)。点P(x,y)是第一象限内的直线上的一个动点(点P不与点E,F重合).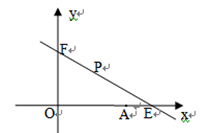
(1)求k的值;
(2)在点P运动的过程中,求出△OPA的面积S与x的函数关系式.
(3)若△OPA的面积为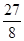 ,求此时点P的坐标.
,求此时点P的坐标.