如图,⊙O的直径AB=4,C为圆周上一点,AC=2,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点 E. 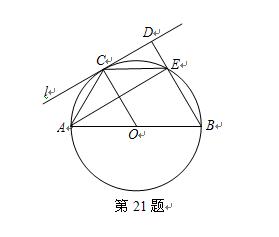
(1). 求∠AEC的度数;
(2). 求证:四边形OBEC是菱形.
在平面直角坐标系中,点A,B的坐标分别为(4,0),(0,4),直线y=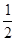 x+b和线段AB交于点D,DE⊥x轴,垂足为点E,DF⊥y轴,垂足为点F,记w=DF﹣DE,当1≤w≤2时,求b的取值范围.
x+b和线段AB交于点D,DE⊥x轴,垂足为点E,DF⊥y轴,垂足为点F,记w=DF﹣DE,当1≤w≤2时,求b的取值范围.
如图,在四边形ABCD中,∠ABC=90°,∠BAD=135°,AB=1,AC= ,点E为CD中点.
,点E为CD中点.
求证:CD=2AE.
在同一平面直角坐标系中,观察以下直线:y=2x,y=﹣x+6,y=x+2,y=4x﹣4图象的共同特点,若y=kx+5也有该特点,试求满足条件的k值.
甲、乙两商场春节期间都进行让利酬宾活动.其中,甲商场对一次购物中超过200元后的价格部分打7折,如图所示,表示甲商场在让利方式下y关于x的函数图象,x(单位:元)表示商品原价,y(单位:元)表示购物金额.若乙商场所有商品按8折出售,请在同一坐标系下画出乙商场在让利方式下y关于x的函数图象,并说明如何选择这两家商场购物更省钱.
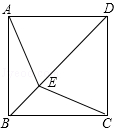
如图,在正方形ABCD中,点E是对角线BD上的点,求证:△ABE≌△CBE.