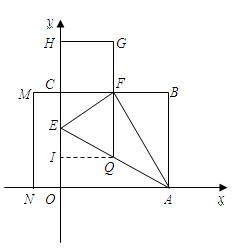
如图所示,将矩形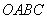 沿
沿 折叠,使点
折叠,使点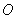 恰好落在
恰好落在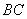 上
上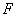 处,以
处,以 为边作正方形
为边作正方形 ,延长
,延长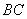 至
至 ,使
,使 ,再以
,再以 、
、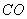 为边作矩形
为边作矩形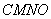 .
.
(1). 试比较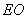 、
、 的大小,并说明理由.
的大小,并说明理由.
(2). 令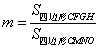 ,请问
,请问 是否为定值?若是,请求出
是否为定值?若是,请求出 的值;若不是,请说明理由.
的值;若不是,请说明理由.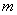 为定值.
为定值.
(3). 在(2)的条件下,若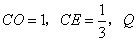 为
为 上一点且
上一点且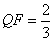 ,抛物线
,抛物线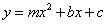 经过
经过 、
、 两点,请求出此抛物线的解析式.
两点,请求出此抛物线的解析式.
(4). 在(3)的条件下,若抛物线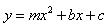 与线段
与线段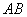 交于点
交于点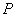 ,试问在直线
,试问在直线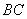 上是否存在点
上是否存在点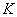 ,使得以
,使得以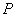 、
、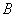 、
、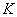 为顶点的三角形与
为顶点的三角形与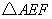 相似?若存在,请求直线
相似?若存在,请求直线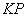 与
与 轴的交点
轴的交点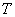 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(·温州市 第21题 10分)如图,AB是半圆O的直径,CD⊥AB于点C,交半圆于点E, DF切半圆于点F。已知∠AEF=135°。
(1)求证:DF∥AB;
(2)若OC=CE,BF=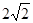 ,求DE的长。
,求DE的长。
(·台州市 第22题 12分)如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC
(1)若∠CBD=39°,求∠BAD的度数
(2)求证:∠1=∠2
(·丽水市 第21题 8分)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O 的切线DF,交AC于点F。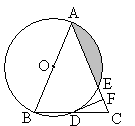
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积。
(·湖州市 第20题 8分)如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连结DE.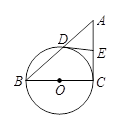
(1)若AD=DB,OC=5,求切线AC的长.
(2)求证:ED是⊙O的切线.
(·绍兴市 第23题 12分)
正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图。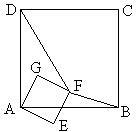
(1)若α=0°,则DF=BF,请加以证明;
(2)试画一个图形(即反例),说明(1)中命题的逆命题是假命题;
(3)对于(1)中命题的逆命题,如果能补充一个条件后能使该逆命题为真命题,请直接写出你认为需要补充的一个条件,不必说明理由。