在平面直角坐标系
中，已知以O为圆心的圆与直线
恒有公共点，且要求使圆O的面积最小.
（1）写出圆O的方程；
（2）圆O与x轴相交于A、B两点，圆内动点P使
、
、
成等比数列，求
的范围；
（3）已知定点Q（−4，3），
直线
与圆O交于M、N两点，试判断
是否有最大值，若存在求出最大值，并求出此时直线的方程，若不存在，给出理由.
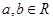，求证：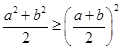
已知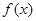
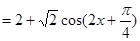的图象向左平移
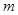个单位（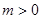
），得到的图象关于直线
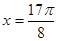对称.
（Ⅰ）求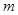的最小值。
（Ⅱ）若方程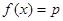
在（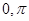
）内有两个不相等的实根
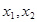，求实数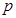
的取值范围及
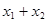的值.
是否存在实数a，使得函数y=sin2x+acosx+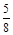
a-
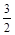在闭区间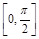
上的最大值是1？若存在，求出对应的a值；若不存在，说明理由.
将一颗质地均匀的正方体骰子（六个面的点数分别为1，2，3，4，5，6）先后抛掷两次，将得到的点数分别记为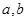
.
（Ⅰ）求直线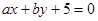
与圆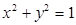
相切的概率；
（Ⅱ）将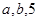
的值分别作为三条线段的长，求这三条线段能围成等腰三角形的概率．
晚会上，主持人面前放着A、B两个箱子，每箱均装有三个球，各箱的三个球分别标有号码1，2，3. 现主持人从A、B两箱中各摸出一球.
（Ⅰ）若用x、y分别表示从A、B两箱中摸出的球的号码，请写出数对(x,y)的所有情形，并回答一共有多少种；
（Ⅱ）求所摸出的两球号码之和为5的概率；
（Ⅲ）如果请你猜摸出的这两球的号码之和，并且猜中有奖，那么猜什么数获奖的可能性最大？说明理由.