如图所示,某货场需将质量m1=100 kg的货物(可视为质点)从高处运送至地面,为避免货物与地面发生撞击,现利用固定于地面的光滑四分之一圆轨道,使货物由轨道顶端无初速度滑下,轨道半径R=1.8 m.地面上紧靠轨道依次排放两块完全相同的木板A、B,长度均为L=2 m,质量均为m2=100 kg,木板上表面与轨道末端相切.货物与木板间的动摩擦因数为μ1,木板与地面间的动摩擦因数μ2=0.2.(最大静摩擦力与滑动摩擦力大小相等)
求货物到达圆轨道末端时对轨道的压力大小和方向。
若货物滑上木板A时,木板不动,而滑上木板B时,木板B开始滑动,求μ1应满足的条件.
若μ1=0.5,求货物滑到木板A末端时的速度和在木板A上运动的时间.
(6分)光纤通信是70年代以后发展起来的新兴技术,世界上许多国家都在积极研究和发展这种技术.发射导弹时,可在导弹后面连一根细如蛛丝的光纤,就像放风筝一样,这种纤细的光纤在导弹和发射装置之间,起着双向传输信号的作用.光纤制导的下行光信号是镓铝砷激光器发出的在纤芯中波长为0.85 的单色光.上行光信号是铟镓砷磷发光二极管发射的在纤芯中波长为1.06
的单色光.上行光信号是铟镓砷磷发光二极管发射的在纤芯中波长为1.06 的单色光.这样操纵系统通过这根光纤向导弹发出控制指令,导弹就如同长“眼睛”一样盯住目标.根据以上信息,回答下列问题:
的单色光.这样操纵系统通过这根光纤向导弹发出控制指令,导弹就如同长“眼睛”一样盯住目标.根据以上信息,回答下列问题:
①在光纤制导中,上行光信号在真空中波长是多少?
②为什么上行光信号和下行光信号要采用两种不同频率的光?(已知光纤纤芯的折射率为1.47)
一定量的气体内能增加了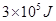 .①若吸收了
.①若吸收了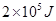 的热量,则是气体对外界做功,还是外界对气体做功?做了多少焦耳的功?②若气体对外界做了
的热量,则是气体对外界做功,还是外界对气体做功?做了多少焦耳的功?②若气体对外界做了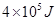 的功,则是气体放热还是从外界吸热?放出或吸收的热量是多少?
的功,则是气体放热还是从外界吸热?放出或吸收的热量是多少?
一质量为 电荷量
电荷量 的与外界绝缘物块A(可视为质点),置于光滑水平面上。A与弹簧左端相连接,弹簧右端固定在竖直墙面上,整个空间中存在水平向右的匀强电场,场强
的与外界绝缘物块A(可视为质点),置于光滑水平面上。A与弹簧左端相连接,弹簧右端固定在竖直墙面上,整个空间中存在水平向右的匀强电场,场强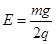 ,平衡时弹簧的压缩量为
,平衡时弹簧的压缩量为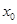 .如图O为弹簧原长时的位置,另一个质量也为
.如图O为弹簧原长时的位置,另一个质量也为 电量为
电量为 的绝缘带电物块B(可视为质点),从O点左侧距离O为
的绝缘带电物块B(可视为质点),从O点左侧距离O为 处的P点由静止释放,当它打在A物块上时立即与A一起向右运动,但不粘连,它们到达最右端后又向左运动,试求:物块B向左运动达到最远点时距O点的距离?(AB相撞在瞬间完成,电荷无转移,不计AB间库仑力,弹簧始终在弹性限度内)。
处的P点由静止释放,当它打在A物块上时立即与A一起向右运动,但不粘连,它们到达最右端后又向左运动,试求:物块B向左运动达到最远点时距O点的距离?(AB相撞在瞬间完成,电荷无转移,不计AB间库仑力,弹簧始终在弹性限度内)。
利用电场和磁场,可以将比荷不同的离子分开,这种方法在化学分析和原子核技术等领域有重要的应用。如图所示的矩形区域ACDG(AC边足够长)中存在垂直于纸面的匀强磁场,A处有一狭缝。离子源产生的离子,经静电场加速后穿过狭缝沿垂直于GA边且垂直于磁场的方向射入磁场,运动到GA边,被相应的收集器收集。整个装置内部为真空。已知被加速的两种正离子的质量分别是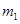 和
和
 ,电荷量均为
,电荷量均为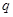 .加速电场的电势差为
.加速电场的电势差为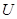 ,离子进入电场时的初速度可以忽略.不计重力,也不考虑离子间的相互作用。
,离子进入电场时的初速度可以忽略.不计重力,也不考虑离子间的相互作用。
(1)求质量为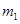 的离子进入磁场时的速率
的离子进入磁场时的速率 ;
;
(2)当磁感应强度的大小为B时,求两种离子在GA边落点的间距 .
.
如图所示,一光滑斜面固定在水平地面上,质量m=1kg的物体在平行于斜面向上的恒力F作用下,从A点由静止开始运动,到达B点时立即撤去拉力F.此后,物体到达C点时速度为零。每隔0.2s通过传感器测得物体的瞬时速度,下表给出了部分测量数据。求:
(1)恒力F的大小。(2)撤去外力F的时刻。