一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球2个,黄球1个.若从中任意摸出一个球,这个球是白球的概率为0.5.
(1)求口袋中红球的个数.
(2)小明认为口袋中共有三种颜色的球,所以从袋中任意摸出一球,摸到红球、白球或黄球的概率都是 ,你认为对吗?请你用列表或画树状图的方法说明理由.
,你认为对吗?请你用列表或画树状图的方法说明理由.
如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1,∠BAE=30°.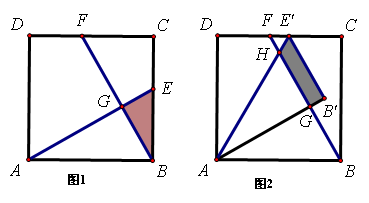
(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB'E'(如图2),使点E落在CD边上的点E'处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
某衬衣店将进价为30元的一种衬衣以40元售出,平均每月能售出600件,调查表明:这种衬衣售价每上涨1元,其销售量将减少10件.
(1)写出月销售利润y(单位:元)与售价x(单位:元/件)之间的函数解析式.
(2)当销售价定为45元时,计算月销售量和销售利润.
(3)衬衣店想在月销售量不少于300件的情况下,使月销售利润达到10000元,销售价应定为多少?
(4)当销售价定为多少元时会获得最大利润?求出最大利润.
如图,点B在 的直径AC的延长线上,点D在
的直径AC的延长线上,点D在 上,AD=DB,∠B=30°,若
上,AD=DB,∠B=30°,若 的半径为4.
的半径为4.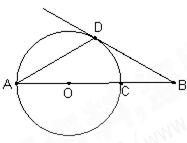
(1)求证:BD是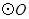 的切线;(2)求CB的长.
的切线;(2)求CB的长.
学校计划用地面砖铺设教学楼前矩形广场的地面ABCD已知矩形广场地面的长为100米,宽为80米.图案设计如图所示:广场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,阴影部分铺绿色地面砖,其余部分铺白色地面砖.
(1)要使铺白色地面砖的面积为5200平方米,则矩形广场四角的小正方形的边长为多少米?
(2)如果铺白色地面砖的费用为每平方米30元,铺绿色地面砖的费用为每平方米20元.当广场四角小正方形的边长为多少米时,铺广场地面的总费用最少?最少费用是多少?
已知:二次函数y=x2+bx-3的图象经过点A(2,5).
(1)求二次函数的解析式;
(2)求二次函数的图象与x轴的交点坐标;
(3)将(1)中求得的函数解析式用配方法化成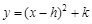 的形式.
的形式.