学校计划用地面砖铺设教学楼前矩形广场的地面ABCD已知矩形广场地面的长为100米，宽为80米.图案设计如图所示：广场的四角为小正方形，阴影部分为四个矩形，四个矩形的宽都为小正方形的边长，阴影部分铺绿色地面砖，其余部分铺白色地面砖.
（1）要使铺白色地面砖的面积为5200平方米，则矩形广场四角的小正方形的边长为多少米？
（2）如果铺白色地面砖的费用为每平方米30元，铺绿色地面砖的费用为每平方米20元.当广场四角小正方形的边长为多少米时，铺广场地面的总费用最少？最少费用是多少？
如图，梯形ABCD中，AD∥BC，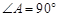
，BC=2，
，
．
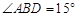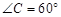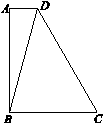
(1) 求∠BDC的度数； (2) 求AB的长．
某采摘农场计划种植
两种草莓共6亩，根据表格信息，解答下列问题：
 项目品种 |
A |
B |
| 年亩产（单位：千克） |
1200 |
2000 |
| 采摘价格（单位：元/千克） |
60 |
40 |
(1)若该农场每年草莓全部被采摘的总收入为46000O元，那么两种草莓各种多少亩?
(2)若要求种植
种草莓的亩数不少于种植
种草莓的一半，那么种植种草莓多少亩时，可使该农场每年草莓全部被采摘的总收入最多?
已知：如图，AB∥CD，AB=CD，点E、F在线段AD上，且AF=DE．求证：BE=CF．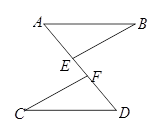
如图，已知直线
与
轴，
轴分别相交于点
．点
从点
出发沿射线
以每秒1个单位长的速度匀速运动，同时点
从点
出发沿
以每秒1个单位长的速度向点
匀速运动．当点到达点时停止运动，点也随之停止.连结
，
交轴于点
.记的中点
关于轴的对称点为
.设点
运动的时间是秒（
）．
（1）当
时，则
＝，点的坐标为；
（2）当
时，若记四边形BDCO的面积为S，则求S关于的函数解析式
（3）当直线EF与△ABO的一边垂直时，求的值；
（4）当
为等腰直角三角形时，请直接写出的值
宏远商贸公司有A、B两种型号的商品需运出，这两种商品的体积和质量分别如下表所示：
| 体积（m3／件） |
质量（吨／件） |
|
| A型商品 |
0.8 |
0.5 |
| B型商品 |
2 |
1 |
（1）已知一批商品有A、B两种型号，体积一共是20 m3 ,质量一共是10.5吨，直接写出A型号商品有件；B两种型号商品有件。
（2）物流公司现有可供使用的货车每辆额定载重3.5吨，容积为6 m3,其收费方式有以下两种：
①按车收费：每辆车运输货物到目的地收费600元；
②按吨收费：每吨货物运输到目的地收费200元.
要将（1）中的商品一次或分批运输到目的地，宏远商贸公司应如何选择运送、付费方式运费最少?并求出该方式下的运费是多少元？