宏远商贸公司有A、B两种型号的商品需运出，这两种商品的体积和质量分别如下表所示：
| |
体积（m3／件） |
质量（吨／件） |
| A型商品 |
0.8 |
0.5 |
| B型商品 |
2 |
1 |
（1）已知一批商品有A、B两种型号，体积一共是20 m3 ,质量一共是10.5吨，直接写出A型号商品有 件；B两种型号商品有 件。
（2）物流公司现有可供使用的货车每辆额定载重3.5吨，容积为6 m3,其收费方式有以下两种：
①按车收费：每辆车运输货物到目的地收费600元；
②按吨收费：每吨货物运输到目的地收费200元.
要将（1）中的商品一次或分批运输到目的地，宏远商贸公司应如何选择运送、付费方式运费最少?并求出该方式下的运费是多少元？
某蔬菜基地，一年中修建了一些蔬菜大棚，平均每公顷修建大棚要用的支架、塑料膜等固定材料的费用为27000元，此外还要购置喷灌设备，这项费用（元）与大棚面积（公顷）的平方成正比，比例系数为9000，每公顷大棚的年平均毛收入为75000元．(1)若
该基地一年中的纯收益（扣除修建费用后）为60000元．一年中该基地修建了多少公顷蔬菜大棚？(2)若要使纯收益达到最大，请问应修建多少公顷大棚？并说明理由．
如图，△ABC内接于⊙O，AB＝AC，弦AD交BC于点E，AE＝4，ED＝5．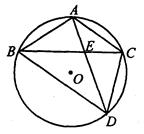
(1)求证：AD平分∠BDC；
(2)求AC的长；
(3)若∠BCD的平分线CI与AD相交于点I，求证：AI＝AC．
（
本题满分8分）已知抛物线y＝x2＋(b－1)x＋c经过点P(－1，－2b)，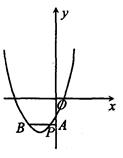
(1)求b＋c的值；
(2)若b＝3，求这条抛物线的顶点坐标；
(3)若b>3，过点P作直线PA⊥y轴，交y轴于点A，交抛物线于另一点B，且BP＝2PA，求这条抛物线所对应的二次函数关系式．
如图，AB为⊙O的直径，点C在⊙O上，过点C作⊙O的切线交AB的延长线于点D，已知∠D＝30°．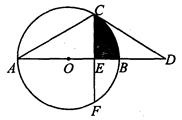
(1)求∠A的度数；
(2)若点F在⊙O上，CF⊥AB，垂足为E，CF＝8
，
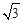求图中阴影部分的面积（结果保留π及根号）．
如图，有一段斜坡BC长为10米，坡角∠CBD＝12°，为方便残疾人的轮椅车通行，现准备把坡角降为5°．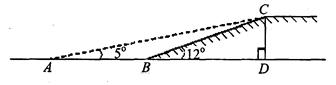
(1)求坡高CD；
(2)求斜坡新起点A与原起点B的距离（精确到0.1米）．
