(本题满分14分,第(1)小题7分,第(2)小题7分)
某地发生特大地震和海啸,使当地的自来水受到了污染,某部门对水质检测后,决定往水中投放一种药剂来净化水质。已 知每投放质量为
知每投放质量为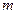 的药剂后,经过
的药剂后,经过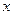 天该药剂在水中释放的浓度
天该药剂在水中释放的浓度 (毫克/升) 满足
(毫克/升) 满足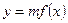 ,其中
,其中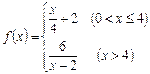 ,当药剂在水中释放的浓度不低于
,当药剂在水中释放的浓度不低于 (毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于
(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于 (毫克/升) 且不高于10(毫克/升)时称为最佳净化。
(毫克/升) 且不高于10(毫克/升)时称为最佳净化。
(1)如果投放的药剂质量为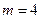 ,试问自来水达到有效净化一共可持续几天?
,试问自来水达到有效净化一共可持续几天?
(2)如果投放的药剂质量为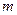 ,为了使在7天之内(从投放药剂算起包括7天)的自来水达到最佳净化,试确定应该投放的药剂质量
,为了使在7天之内(从投放药剂算起包括7天)的自来水达到最佳净化,试确定应该投放的药剂质量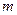 的值。
的值。
(本小题满分14分)已知函数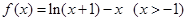 .
.
(1)求 的单调区间;
的单调区间;
(2)已知数列 的通项公式为
的通项公式为 ,求证:
,求证: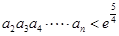 (
( 为自然对数的底数);
为自然对数的底数);
(3)若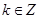 ,且
,且 对任意
对任意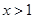 恒成立,求
恒成立,求 的最大值
的最大值
(本小题满分13分)已知等差数列 的前
的前 项和为
项和为 ,并且
,并且 ,
,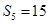 ,数列
,数列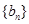 满足:
满足: ,
, ,记数列
,记数列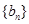 的前
的前 项和为
项和为 .
.
(1)求数列 的通项公式
的通项公式 及前
及前 项和公式
项和公式 ;
;
(2)求数列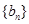 的通项公式
的通项公式 及前
及前 项和公式
项和公式 ;
;
(3)记集合 ,若
,若 的子集个数为16,求实数
的子集个数为16,求实数 的取值范围
的取值范围
(本小题满分12分)已知 的角
的角 所对的边分别是
所对的边分别是 ,设向量
,设向量 ,
,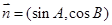 ,
, .
.
(1)若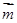 ∥
∥ ,求角B的大小;
,求角B的大小;
(2)若 ,边长
,边长 ,求
,求 的面积的最大值.
的面积的最大值.
(本小题满分12分) 已知函数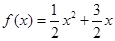 ,,数列
,,数列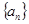 的前
的前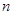 项和为
项和为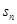 ,点
,点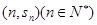 均在函数
均在函数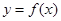 的图象上.
的图象上.
(1)求数列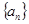 的通项公式
的通项公式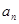 ;
;
(2)令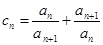 ,证明:
,证明: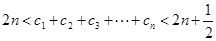 .
.
本小题满分12分)已知集合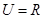 ,集合
,集合 ,函数
,函数 的定义域为集合B.
的定义域为集合B.
(1)若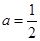 ,求集合
,求集合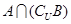 ;
;
(2)命题 ,命题
,命题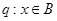 ,若
,若 是
是 的必要条件,求实数
的必要条件,求实数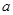 的取值范围.
的取值范围.