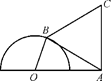
(本题满分15分) 设椭圆C1：
的左、右焦点分别是F1、F2，下顶点为A，线段OA
的中点为B（O为坐标原点），如图．若抛物线C2：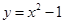
与y轴的交点为B，且经过F1，F2点．
（Ⅰ）求椭圆C1的方程；
（Ⅱ）设M（0，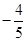
），N为抛物线C2上的一动点，过点N作抛物线C2的切线交椭圆C1于P、Q两点，求
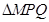面积的最大值．
如图，△ABC中，在AC上取一点N，使AN＝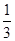
AC；在AB上取一点M，使得AM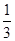＝AB；在BN的延长线上取点P，使得NP＝
BN；在CM的延长线上取点Q，使得
＝λ
时，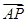
＝
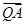，试确定λ的值．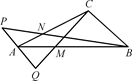
设两个非零向量a与b不共线．
(1)若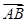
＝a＋b，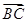
＝2a＋8b，
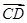＝3(a－b)．求证：A、B、D三点共线；
(2)试确定实数k，使ka＋b和a＋kb共线．
在△ABC中，E、F分别为AC、AB的中点，BE与CF相交于G点，设
＝a，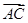
＝b，试用a，b表示
.
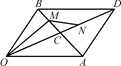
平行四边形OADB的对角线交点为C，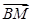
＝
，
＝
，
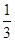
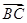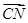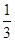
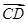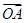＝a，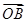
＝b，用a、b表示
、
、
.
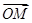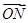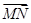如图，半圆O的直径为2，A为直径延长线上的一点，OA＝2，B为半圆上任意一点，以AB为一边作等边三角形ABC.问：点B在什么位置时，四边形OACB面积最大？