:甲、乙两同学投掷一枚骰子,用字母p、q分别表示两人各投掷一次的点数.(1)求满足关于x的方程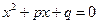 有实数解的概率.
有实数解的概率.
(2)求(1)中方程有两个相同实数解的概率.
如图,⊙H与x轴交于A、B两点,与y轴交于C、D两点,圆心H的坐标是(1,﹣1),半径是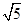 .
.
(1)求经过点D的切线的解析式;
(2)问过点A的切线与过点D的切线是否垂直?若垂直,请写出证明过程;若不垂直,请说明理由.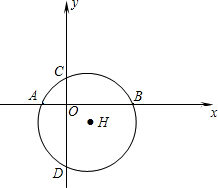
已知定点F(0,﹣2),动点P(x,y)到F点的距离与它到x轴的距离相等.
(1)写出y关于x的函数关系式;
(2)若(1)中的函数图象与过F点的直线y=kx+b交于A、B两点,
ⅰ请用k表示线段AB的长;
ⅱ以AB为弦的圆与y轴交于M(0,﹣4+2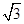 )、N(0,﹣4﹣2
)、N(0,﹣4﹣2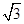 )两点,求此时直线y=kx+b的解析式.
)两点,求此时直线y=kx+b的解析式.
已知n为正整数,一次函数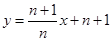 的图象与坐标轴围成的三角形外接圆面积为
的图象与坐标轴围成的三角形外接圆面积为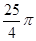 .求此一次函数的解析式.
.求此一次函数的解析式.
如图,△ABC中,∠C=Rt∠,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?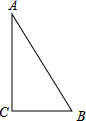
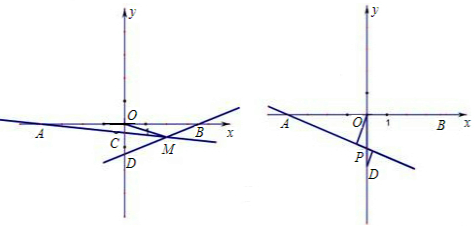
如左图:直线y=kx+4k(k≠0)交x轴于点A,交y轴于点C,点M(2,m)为直线AC上一点,过点M的直线BD交x轴于点B,交y轴于点D.
(1)求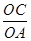 的值(用含有k的式子表示.);
的值(用含有k的式子表示.);
(2)若S△BOM=3S△DOM,且k为方程(k+7)(k+5)﹣(k+6)(k+5)=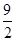 的根,求直线BD的解析式.
的根,求直线BD的解析式.
(3)如右图,在(2)的条件下,P为线段OD之间的动点(点P不与点O和点D重合),OE上AP于E,DF上AP于F,下列两个结论:①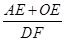 值不变;②
值不变;②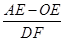 值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值.
值不变,请你判断其中哪一个结论是正确的,并说明理由并求出其值.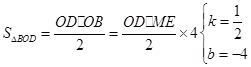
 .
.