若矩形的一个短边与长边的比值为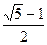
，（黄金分割数），我们把这样的矩形叫做黄金矩形
（1） 操作：请你在如图15所示的黄金矩形ABCD（AB＞AD）中，以短边AD为一边作正方形AEFD。
（2） 探究：在（1）中的四边形EBCF是不是黄金矩形？若是，请予以证明；若不是，请说明理由。
（3） 归纳：通过上述操作及探究，请概括出具体有一般性的结论（不需证明）
如图，△ABC平移后的图形是△A′B′C′，其中C和C′是对应点，请画出平移后的三角形A′B′C′．
某学校准备在升旗台的台阶上铺设一种红色的地毯(含台阶的最上层)，已知这种地毯的批发价为每平方米40元，升旗台的台阶宽为3米，其侧面如图所示．请你帮助测算一下，买地毯至少需要多少元？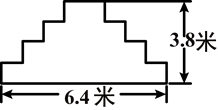
如图，在长方形ABCD中，AB＝10cm，BC＝6cm，试问将长方形ABCD沿着AB方向平移多少才能使平移后的长方形EFGH与原来的长方形ABCD重叠部分的面积为24cm2？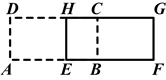
如图，AD∥BC，EF∥AD，CE平分∠BCF，∠DAC＝120°，∠ACF＝20°，求∠FEC的度数．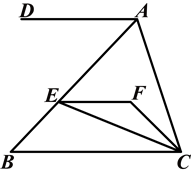
如图，已知直线l1∥l2，直线l3和直线l1，l2交于点C和点D，在直线CD上有一点P．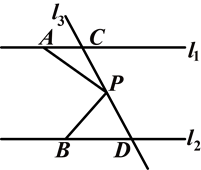
(1)如果P点在C、D之间运动，问∠PAC，∠APB，∠PBD有怎样的数量关系？请说明理由；
(2)若点P在C、D两点的外侧运动(P点与点C、D不重合)，试探索∠PAC，∠APB，∠PBD之间的关系又是如何．