(本小题满分14分)若函数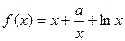 ,
,
(1)当 时,求函数
时,求函数 的单调增区间;
的单调增区间;
(2)函数 是否存在极值.
是否存在极值.
已知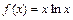 .
.
(1)求函数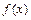 在区间
在区间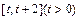 上的最小值;
上的最小值;
(2)对一切实数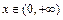 ,
,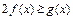 恒成立,求实数
恒成立,求实数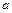 的取值范围;
的取值范围;
(3)证明对一切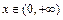 ,
,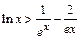 恒成立.
恒成立.
设椭圆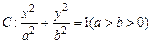 的左焦点为
的左焦点为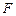 ,过点
,过点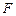 的直线与椭圆
的直线与椭圆 相交于
相交于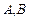 两点,直线
两点,直线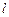 的倾斜角为60o,
的倾斜角为60o,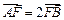 .
.
(1)求椭圆 的离心率;
的离心率;
(2)如果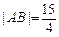 ,求椭圆
,求椭圆 的方程
的方程
张家界某景区为提高经济效益,现对某一景点进行改造升级,从而扩大内需,提高旅游增加值,经过市场调查,旅游增加值 万元与投入
万元与投入 万元之间满足:
万元之间满足: 为常数。当
为常数。当 万元时,
万元时, 万元;当
万元;当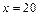 万元时,
万元时,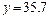 万元。(参考数据:
万元。(参考数据: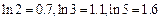 )
)
(1)求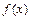 的解析式;
的解析式;
(2)求该景点改造升级后旅游利润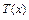 的最大值。(利润=旅游增加值-投入)
的最大值。(利润=旅游增加值-投入)
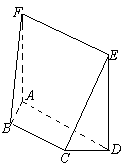
如图,在五面体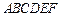 中,四边形
中,四边形 是正方形,
是正方形,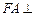 平面
平面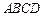 ,
, ∥
∥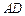 ,
,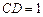 ,
, 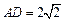 ,
, 。
。
(Ⅰ)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(Ⅱ)证明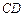 ⊥平面
⊥平面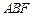 ;
;
(Ⅲ)求二面角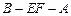 的正切值
的正切值
某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为 .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。
(1)求甲中奖且乙、丙都没有中奖的概率;
(2)求中奖人数ξ的分布列及数学期望Eξ