已知向量 =(1,1),向量
=(1,1),向量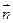 与向量
与向量 的夹角为
的夹角为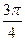 ,且
,且 ·
·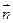
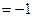 .
.
(1)求向量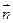 ;
;
(2)若向量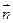 与向量
与向量 = (1,0)的夹角为
= (1,0)的夹角为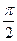 ,向量
,向量 =(
=(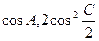 ),其中A,C是△ABC的内角,且A,B,C依次成等差数列,试求|
),其中A,C是△ABC的内角,且A,B,C依次成等差数列,试求|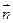 +
+ |的取值范围.
|的取值范围.
旅游公司为3个旅游团提供4条旅游线路,每个旅游团任选其中一条. 
(1)求3个旅游团选择3条不同的线路的概率
(2)求恰有2条线路没有被选择的概率.
(3)求选择甲线路旅游团数的期望.
已知向量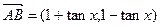 ,
,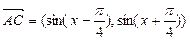 .
.
(1)求证: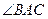 为直角;
为直角;
(2)若 ,求
,求 的边
的边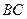 的长度的取值范围.
的长度的取值范围.
已知函数 的定义域为
的定义域为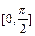 ,值域为[-5,4];函数
,值域为[-5,4];函数  .
.
(Ⅰ) 求函数g(x)的最小正周期和最大值;
(Ⅱ) 当 , 且g(x) =5时, 求tan x.
, 且g(x) =5时, 求tan x.
甲、乙两人进行某项对抗性游戏,采用“七局四胜”制,即先赢四局者为胜,若甲、乙两人水平相当,且已知甲先赢了前两局,求:
(1)乙取胜的概率;
(2)比赛进行完七局的概率。
(3)记比赛局数为 ,求
,求 的分布列为数学期望
的分布列为数学期望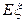 .
.