某同学打算骑自行车到野生动物园去参观,出发时心里盘算,如果以每小时8千米的速度骑行,那么中午12点才能到达;如果以每小时12千米的速度骑行,那么10点就能到达;但最好是不快不慢恰好在11点到达,那么,他行驶的速度是多少最好呢?
如图所示,在⊙O中,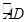 =
=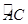 ,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
(1)求证:AC2=AB·AF;
(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分的面积.
如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)若AB=2,∠P=30°,求AP的长;
(2)若D为AP的中点,求证:直线CD是⊙O的切线.
周末,小亮一家在东昌湖游玩,妈妈在湖心岛岸边P处观看小亮与爸爸在湖中划船(如图).小船从P处出发,沿北偏东60°划行200米到达A处,接着向正南方向划行一段时间到达B处.在B处小亮观测妈妈所在的P处在北偏西37°方向上,这时小亮与妈妈相距多少米(精确到米)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ≈1.41,
≈1.41, ≈1.73)
≈1.73)
如图,2012年4月10日,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦查发现,在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民,此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?( ≈1.41,
≈1.41, ≈1.73,
≈1.73, =2.45).
=2.45).
如图,一段河坝的横截面为梯形ABCD,试根据图中数据,求出坝底宽AD.(i=CE∶ED,单位:m)