已知函数 .
.
(1)设 ,求函数
,求函数 的极值;
的极值;
(2)若 ,且当
,且当 时,
时,
 12a恒成立,试确定
12a恒成立,试确定 的取值范围.
的取值范围.
(本小题满分12分)
某校高二年级共有1200名学生,为了分析某一次数学考试情况,今抽查100份试卷,成绩分布如下表:
| 成绩 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 人数 |
4 |
5 |
6 |
9 |
21 |
27 |
15 |
9 |
4 |
| 频率 |
0.04 |
0.05 |
0.06 |
0.09 |
0.21 |
0.27 |
0.15 |
0.09 |
0.04 |
(Ⅰ)画出频率分布直方图;
 |
 |
(Ⅱ)由频率分布表估计这次考试及格(60分以上为及格)的人数;
(Ⅲ)由频率分布直方图估计这考试的平均分.
(本小题满分10分)
(1)用辗转相除法求840与1764的最大公约数.
(2)用更相减损术求 与
与 的最大公约数
的最大公约数
已知点P(-1, )是椭圆E:
)是椭圆E: (
( )上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
)上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
(1)求椭圆E的方程;
(2)设A、B是椭圆E上两个动点, (0<λ<4,且λ≠2).求证:直线AB的斜率等于椭圆E的离心率;
(0<λ<4,且λ≠2).求证:直线AB的斜率等于椭圆E的离心率;
(3)在(2)的条件下,当△PAB面积取得最大值时,求λ的值.
((本小题满分12分)
已知点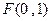 ,一动圆过点
,一动圆过点 且与圆
且与圆 内切.
内切.
(1)求动圆圆心的轨迹 的方程;
的方程;
(2)设点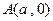 ,点
,点 为曲线
为曲线 上
上 任一点,求点
任一点,求点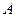 到点
到点 距离的最大值
距离的最大值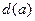 ;
;
(3)在 的条件下,设△
的条件下,设△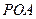 的面积为
的面积为 (
( 是坐标原点,
是坐标原点, 是曲线
是曲线 上横坐标为
上横坐标为 的点),以
的点),以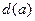 为边长的正方形的面积为
为边长的正方形的面积为 .若正数
.若正数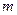 使得
使得 恒成立,问
恒成立,问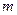 是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
( (本题满分12分)
在一次抗洪抢险中,准备用射击的方法引爆从桥上游漂流而下的一巨大汽油罐.已知
只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功,每次射击命中率都是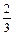 .,每次命中与否互相独立.
.,每次命中与否互相独立.
(1)求油罐被引爆的概率。
(2)如果引爆或子弹打光则停止射击,设射击次数为ξ,求ξ的分布列及ξ的数学期望。