(本小题满分14分
函数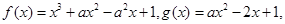 实数
实数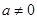 .
.
(I)若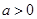 ,求函数
,求函数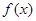 的单调区间;
的单调区间;
(II)当函数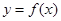 与
与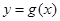 的图象只有一个公共点且
的图象只有一个公共点且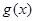 存在最小值时,记
存在最小值时,记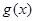 的最小值为
的最小值为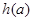 ,求的值域;
,求的值域;
(III)若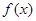 与
与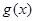 在区间
在区间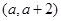 内均为增函数,求
内均为增函数,求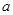 的取值范围。
的取值范围。
(文)已知函数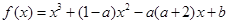
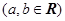 .
.
(I)若函数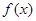 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是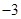 ,求
,求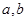 的值;
的值;
(II)若函数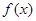 在区间
在区间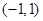 上不单调,求
上不单调,求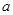 的取值范围
的取值范围
已知函数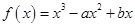 的图象与直线
的图象与直线 相切于点
相切于点 .
.
(1)求实数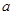 和
和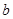 的值;
的值;
(2)求 的极值.
的极值.
已知函数 的反函数为
的反函数为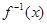 ,设
,设 的图象上在点
的图象上在点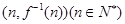 处的切线在y轴上的截距为
处的切线在y轴上的截距为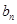 ,数列{
,数列{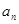 }满足:
}满足: .(1)求数列{
.(1)求数列{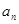 }的通项公式;
}的通项公式;
(2)在数列 中,仅
中,仅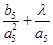 最小,求
最小,求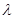 的取值范围;
的取值范围;
(3)令函数 数列
数列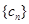 满足
满足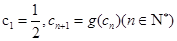 ,求证:对一切n≥2的正整数都有
,求证:对一切n≥2的正整数都有 .
.
如图,椭圆 :
: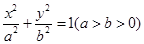 ,
, 、
、 、
、 、
、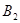 为椭圆
为椭圆 的顶点.
的顶点.
(1)若椭圆 上的点
上的点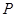 到焦点距离的最大值为
到焦点距离的最大值为 ,最小值为
,最小值为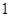 ,求椭圆方程;
,求椭圆方程;
(2)已知:直线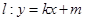 相交于
相交于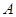 ,
,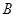 两点(
两点( 不是椭圆的左右顶点),并满足
不是椭圆的左右顶点),并满足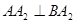 .试研究:直线
.试研究:直线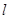 是否过定点? 若过定点,请求出定点坐标,若不过定点,请说明理由.
是否过定点? 若过定点,请求出定点坐标,若不过定点,请说明理由.
在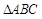 中,已知
中,已知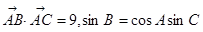 ,又
,又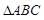 的面积等于6.
的面积等于6.
(1)求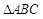 的三边之长;
的三边之长;
(2)设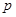 是
是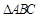 (含边界)内一点,
(含边界)内一点,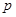 到三边
到三边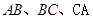 的距离分别为
的距离分别为 ,求
,求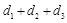 的取值范围.
的取值范围.
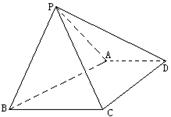
如图,已知四棱锥P-ABCD的底面为直角梯形,AD∥BC,∠BCD=900,
PA=PB,PC=PD.
(1)试判断直线CD与平面PAD是否垂直,并简述理由;
(2)求证:平面PAB⊥平面ABCD;
(3)如果CD=AD+BC,二面角P-CB-A等于600,求二面角P-CD-A的大小.