如图,四边形ABCD是菱形,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F,连接CE.
(1)求证:∠DAE=∠DCE;
(2)当AE=2EF时,判断FG与EF有何等量关系?并证明你的结论?
如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点G。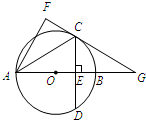
⑴直线FC与⊙O有何位置关系?并说明理由;
⑵若OB=BG=2,求CD的长。
关于x的一元二次方程
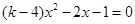 。
。 ⑴若方程有两个不相等的实数根,求k的取值范围;
⑵当k是怎样的正整数方程没有实数根?
某工厂甲、乙两名工人参加操作技能培训。现分别从他们在培训期间参加的若干次测试成绩中随机抽取6次,记录如下:
| 甲 |
79 |
82 |
78 |
81 |
80 |
80 |
| 乙 |
83 |
80 |
76 |
81 |
79 |
81 |
⑴请你计算这两组数据的平均数;
⑵现要从中选派一人参加操作技能比赛,从成绩的稳定性考虑,你认为选派哪名工人参加合适?请说明理由。
如图,一条公路的转弯处是一段圆弧(图中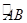 ),点O是这段弧的圆心,C是
),点O是这段弧的圆心,C是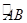 上一点,OC⊥AB,垂足为D,AB=300m,CD=50m,求这段弯路的半径。
上一点,OC⊥AB,垂足为D,AB=300m,CD=50m,求这段弯路的半径。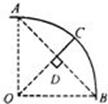
如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C。问:线段CE和线段BF相等吗?请说明理由。