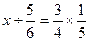（本题6分）随着我国经济的高速发展，有着“经济晴雨表”之称的股市也得到迅速的发展，下表是今年上证指数某一周星期一至星期五的变化情况. （注：上周五收盘时上证指数为2616点，每一天收盘时指数与前一天相比，涨记为“＋”，跌记为“－”）
| 星 期 |
一 |
二 |
三 |
四 |
五 |
| 指数的变化(与前一天比较) |
 |
 |
 |
 |
 |
⑴ 请求出这一周星期五收盘时的上证指数是多少点？
⑵ 说出这一周每一天收盘时上证指数哪一天最高？哪一天最低？分别是多少点？
解方程 (每小题5分，共10分)（1）
（2）
计算：(前3题每小题4分，第（4）题6分，共18分)(1)
(2)
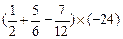
(3)
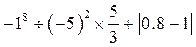
(4)先化简，再求值。
；其中a=—2，b=3
应用题。1、某厂一车间上半年生产零件48万件，是下半年产量的
，该车间全年的产量是多少？2、高铁列车的运行速度是380千米/小时，普通列车的速度是它的
。普通列车的速度是多少？3、用120cm的铁丝做一个长方体框架。长、宽、高的比是3:2:1。这个长方体的体积是多少?
4、一个圆形花坛。周长是25.12m。如果在这个花坛的周围铺上一条宽1m的环形小路，这条小路的面积是多少平方米?
5、校园里有杨树40棵，是柳树的
。松树棵数是柳树的
。松树有多少棵？6、某厂为青海玉树灾区赶制一批帐篷。第一天生产了这批帐篷的
，第二天生产了总数的
。两天共生产4400顶。第一天生产了多少顶？
求阴影部分的面积。（单位：cm）1、外圆半径：5，内圆半径：3
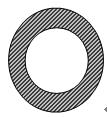
2、d=10（三角形以及直径d下面的部分）
|
解方程。（1）
（2）
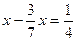
（3）
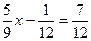
（4）
