(本小题满分10分)
某商场将进价40元一个的某种商品按50元一个售出时,每月能卖出500个.商场想了两个方案来增加利润:
方案一:提高价格,但这种商品每个售价涨价1元,销售量就减少10个;
方案二:售价不变,但发资料做广告。已知这种商品每月的广告费用m(千元)与销售量倍数p关系为p =  ;
;
试通过计算,请你判断商场为赚得更大的利润应选择哪种方案?请说明你判断的理由!
先化简,再求值.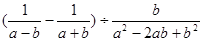 ,其中
,其中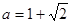 ,
,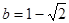
计算:
解方程: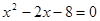
如图,正三角形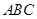 的边长为
的边长为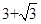 .
.
(1)如图①,正方形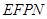 的顶点
的顶点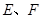 在边
在边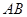 上,顶点
上,顶点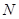 在边
在边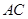 上.在正三角形
上.在正三角形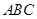 及其内部,以
及其内部,以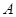 为位似中心,作正方形
为位似中心,作正方形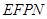 的位似正方形
的位似正方形 ,且使正方形
,且使正方形 的面积最大(不要求写作法);
的面积最大(不要求写作法);
(2)求(1)中作出的正方形 的边长;
的边长;
(3)如图②,在正三角形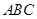 中放入正方形
中放入正方形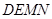 和正方形
和正方形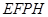 ,使得
,使得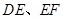 在边
在边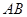 上,点
上,点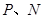 分别在边
分别在边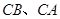 上,求这两个正方形面积和的最大值及最小值,并说明理由.
上,求这两个正方形面积和的最大值及最小值,并说明理由.
(无原图)
如果一条抛物线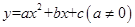 与
与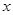 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.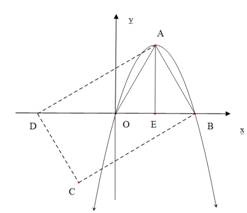
(1)“抛物线三角形”一定是三角形;
(2)若抛物线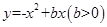 的“抛物线三角形”是等腰直角三角形,求
的“抛物线三角形”是等腰直角三角形,求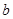 的值;
的值;
(3)如图,△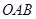 是抛物线
是抛物线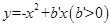 的“抛物线三角形”,是否存在以原点
的“抛物线三角形”,是否存在以原点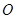 为对称中心的矩形
为对称中心的矩形 ?若存在,求出过
?若存在,求出过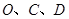 三点的抛物线的表达式;若不存在,说明理由.
三点的抛物线的表达式;若不存在,说明理由.