(本小题满分12分)如图1,已知抛物线经过坐标原点 和
和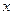 轴上另一点
轴上另一点 ,顶点
,顶点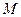 的坐标为
的坐标为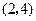 ;矩形
;矩形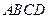 的顶点
的顶点 与点
与点 重合,
重合, 分别在
分别在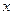 轴、
轴、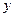 轴上,且
轴上,且 ,
, .
.
(1)求该抛物线所对应的函数关系式;
(2)将矩形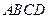 以每秒1个单位长度的速度从图1所示的位置沿
以每秒1个单位长度的速度从图1所示的位置沿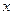 轴的正方向匀速平行移动,同时一动点
轴的正方向匀速平行移动,同时一动点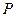 也以相同的速度从点
也以相同的速度从点 出发向
出发向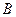 匀速移动.设它们运动的时间为
匀速移动.设它们运动的时间为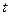 秒(
秒( ),直线
),直线 与该抛物线的交点为
与该抛物线的交点为 (如图2所示).
(如图2所示).
①当 时,判断点
时,判断点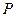 是否在直线
是否在直线 上,并说明理由;
上,并说明理由;
②设以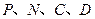 为顶点的多边形面积为
为顶点的多边形面积为 ,试问
,试问 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
如图,在平行四边形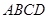 中,以点
中,以点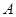 为圆心,
为圆心,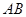 为半径的圆,交
为半径的圆,交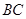 于点
于点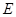 .
.
(1)求证: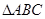 ≌
≌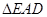 ;
;
(2)如果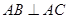 ,
,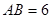 ,
,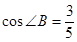 ,求
,求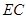 的长.
的长.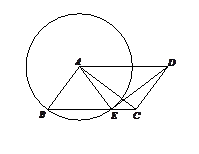
解方程: .
.
已知:如图,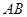 ⊥
⊥ ,
,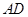 ∥
∥ ,
,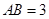 ,
, .点
.点 在线段
在线段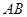 上,联结
上,联结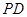 ,过点
,过点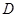 作
作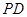 的垂线,与
的垂线,与 相交于点
相交于点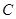 .设线段
.设线段 的长为
的长为 .
.
(1)当 时,求线段
时,求线段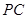 的长;
的长;
(2)设△ 的面积为
的面积为 ,求
,求 关于
关于 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(3)当△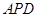 ∽△
∽△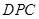 时,求线段
时,求线段 的长.
的长.

已知:如图,抛物线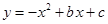 与
与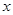 轴的负半轴相交于点
轴的负半轴相交于点 ,与
,与 轴相交于点
轴相交于点 (0,3),且∠
(0,3),且∠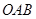 的余切值为
的余切值为 .
.
(1)求该抛物线的表达式,并写出顶点 的坐标;
的坐标;
(2)设该抛物线的对称轴为直线 ,点
,点 关于直线
关于直线 的对称点为
的对称点为 ,
,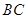 与直线
与直线 相交于点
相交于点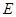 .点
.点 在直线
在直线 上,如果点
上,如果点 是△
是△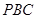 的重心,求点
的重心,求点 的坐标;
的坐标;
(3)在(2)的条件下,将(1)所求得的抛物线沿 轴向上或向下平移后顶点为点
轴向上或向下平移后顶点为点 ,写出平移后抛物线的表达式.点
,写出平移后抛物线的表达式.点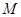 在平移后的抛物线上,且△
在平移后的抛物线上,且△ 的面积等于△
的面积等于△ 的面积的2倍,求点
的面积的2倍,求点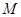 的坐标.
的坐标.
已知:如图,在梯形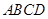 中,
中,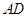 ∥
∥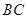 ,点
,点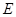 、
、 在边
在边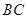 上,
上,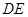 ∥
∥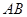 ,
,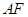 ∥
∥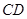 ,且四边形
,且四边形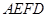 是平行四边形.
是平行四边形.
(1)试判断线段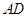 与
与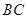 的长度之间有怎样的数量关系?并证明你的结论;
的长度之间有怎样的数量关系?并证明你的结论;
(2)现有三个论断:① ;②∠
;②∠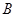 +∠
+∠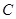 =90°;③∠
=90°;③∠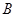 =2∠
=2∠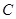 .请从上述三个论断中选择一个论断作为条件,证明四边形
.请从上述三个论断中选择一个论断作为条件,证明四边形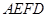 是菱形.
是菱形.