甲、乙两地同时生产某种蔬菜若干吨,现甲地可外销这种蔬菜10吨,乙地可外销这种蔬菜4吨,经调查A、B两城各需这种蔬菜分别为8吨和6吨.每吨这种蔬菜的运费如下表.设乙地运往B城的这种蔬菜为x吨.
(1)用含x的代数式来表示总运费(单位:百元/吨);
(2)若总运费为8400元,则乙地运往A城的这种蔬菜为多少吨?
(3)试问有无可能总运费为7400元?若有可能,请写出相应的调动方案;若无可能,请说明理由.
(本题8分) 在国家的宏观调控下,某市的商品房成交价由今年7月份的14000元/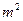 下降到9月份的12600元/
下降到9月份的12600元/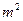
⑴求8、9两月平均每月降价的百分率是多少?(参考数据: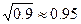 )
)
⑵如果房价继续回落,按此降价的百分率,你预测到11月份该市的商品房成交均价是否会跌破10000元/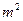 ?请说明理由。
?请说明理由。
(本题8分) 已知:抛物线 与x轴相交于A、B两点(A点在B点的左侧),
与x轴相交于A、B两点(A点在B点的左侧),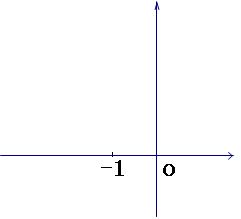
顶点为P.
(1)求A、B、P三点坐标;
(2)画出此抛物线的简图,并根据简图直接写出当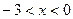 时,函数值y的取值范围;
时,函数值y的取值范围;
(本题8分)关于x的一元二次方程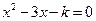 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围.
(2)请选择一个k的负整数值,并求出方程的根.
(每小题6分,共18分)解下列方程:
①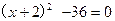 ②
②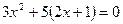
③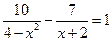
(本题12分)
如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如: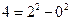 ,
,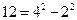 ,
,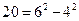 ,因此
,因此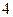 ,
,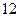 ,
,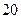 这三个数都是神秘数.
这三个数都是神秘数.
(1)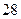 和
和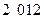 这两个数是神秘数吗?为什么?
这两个数是神秘数吗?为什么?
(2)设两个连续偶数为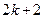 和
和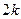 (其中
(其中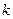 取非负整数),由这两个连续偶数构造的神秘数是
取非负整数),由这两个连续偶数构造的神秘数是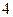 的倍数吗?为什么?
的倍数吗?为什么?
(3)两个连续奇数的平方差(取正数)是神秘数吗?为什么?