(满分l2分)如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)已知PA=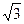 ,BC=1,求⊙O的半径.
,BC=1,求⊙O的半径.
(1)若 +(b-2)2=0,A=3a2-6ab+b2,B=-a2-5,求A-B的值.
+(b-2)2=0,A=3a2-6ab+b2,B=-a2-5,求A-B的值.
(2)试说明:无论x ,y取何值时,代数式
,y取何值时,代数式
(x3+3x2y-5xy+6y3)+(y3+2xy2+x2y-2x3)-(4x2y-x3-3xy2+7y3)的值是常数.
.已知m、x、y满足:(1) , (2)
, (2) 与
与 是同类项.求代数式:
是同类项.求代数式: 的值.
的值.
一个多项式加上 的2倍得
的2倍得 ,求这个多项式
,求这个多项式
先化简,再求值: ,其中
,其中 ,
, 。
。
某电子科技公司开发一种新产品.产品投产上市一年来,公司经历了由初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次).公司前12个月累积获得的利润y(万元)与销售时间第x(月)之间的函数关系(即前x个月的利润总和y与x之间的关系)对应的点都在如图所示的图象上.该图象是某二次函数y=a(x-h)2+k图象的一部分,点A为抛物线的顶点,且点A,B,C的横坐标分别为4,10,12,点A,B的纵坐标分别为-16,20.
(1)求前12个月该公司累积获得的利润y(万元)与时间第x(月)之间的函数关系式;
(2)分别求出前9个月公司累积获得的利润和10月份一个月内所获得的利润;
(3)在前12个月中,哪个月该公司一个月内所获得的利润最多?最多利润是多少万元?
 |