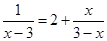(满分l4分)如图，在Rt△ABC中，∠C=90°，AC=3，AB=5．点P从点C出发沿CA以每秒1个单位长度的速度向点A匀速运动，到达点A后立刻以原来的速度沿AC返回；点Q从点A出发沿AB以每秒1个单位长度的速度向点B匀速运动．伴随着P，Q的运动，DE保持垂直平分PQ，且交PQ于点D，交折线QB—BC—CP于点E．点P，Q同时出发，当点Q到达点B时停止运动，点P也随之停止．设点P，Q运动的时间是t s(t>O)．
(1)当t=2时，AP=________，点Q到AC的距离是_________；
(2)在点P从C向A运动的过程中，求△APQ的面积S与t的函数关系式；(不必写出t的取值范围)
(3)在点E从B向C运动的过程中，四边形QBED能否成为直角梯形?若能，请求出t的值；若不能，也请说明理由．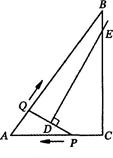
清明节期间，文笔中学团委组织八年级部分学生去离校2.4千米的玉泉山烈士陵园扫墓，回来时乘公交车所花时间比去时步行少用了36分钟，已知公交车速度是学生步行速度的5倍，求学生的步行速度．
已知一个反比例函数的图象经过点
．
（Ⅰ）求这个函数的解析式；
（Ⅱ）判断点
是否在这个函数的图象上；
（Ⅲ）当
时，求自变量
的值．
《中华人民共和国道路交通管理条例》规定：小汽车在城市街道上行驶速度不得超过
千米/小时，如图，一辆小汽车在一条城市街道上直道行驶，某一时刻刚好行驶到路对面车速检测仪
正前方
米点
处，过了
秒后，小汽车在点
处测得与车速检测仪间距离为
米，问：这辆小汽车超速了吗？
先化简，再选取一个你喜欢的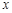
值，代入求值：
．
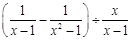（Ⅰ）化简：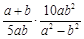
；
（Ⅱ）解分式方程：