《中华人民共和国道路交通管理条例》规定:小汽车在城市街道上行驶速度不得超过 千米/小时,如图,一辆小汽车在一条城市街道上直道行驶,某一时刻刚好行驶到路对面车速检测仪
千米/小时,如图,一辆小汽车在一条城市街道上直道行驶,某一时刻刚好行驶到路对面车速检测仪 正前方
正前方 米点
米点 处,过了
处,过了 秒后,小汽车在点
秒后,小汽车在点 处测得与车速检测仪
处测得与车速检测仪 间距离为
间距离为 米,问:这辆小汽车超速了吗?
米,问:这辆小汽车超速了吗?
如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△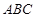 的三个顶点都在格点上.
的三个顶点都在格点上.
(1)建立如图所示的直角坐标系,请在图中标出△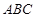 的外接圆的圆心
的外接圆的圆心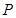 的位置,并填写:
的位置,并填写:
①圆心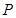 的坐标:
的坐标: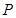 (_______,_______);
(_______,_______);
②⊙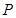 的半径为_______ .
的半径为_______ .
(2)将△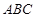 绕点
绕点 逆时针旋转
逆时针旋转 得到△
得到△ ,画出图形,并求线段
,画出图形,并求线段 扫过的图形的面积.
扫过的图形的面积.
某同学作业本上做了这么一道题:“当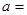
 时,试求
时,试求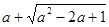 的值”,其中
的值”,其中 是被墨水污染的,该同学得出代数式的答案为
是被墨水污染的,该同学得出代数式的答案为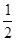 ,请判断该同学答案是否正确,说出你的道理.
,请判断该同学答案是否正确,说出你的道理.
小林准备进行如下操作实验:把一根长为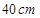 的铁丝剪成两段,并把每一段各围成一个正方形.
的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于 ,小林该怎么剪?
,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于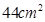 .”他的说法对吗?请说明理由.
.”他的说法对吗?请说明理由.
小明、小丽两位同学八年级10次数学单元自我检测的成绩(成绩均为整数,且个位数为0)分别如下图所示:
(1)根据上图中提供的数据填写下表:
| 平均成绩 |
中位数 |
众数 |
方差(S2) |
|
| 小明 |
80 |
80 |
||
| 小丽 |
85 |
260 |
(2)如果将90分以上(含90分)的成绩视为优秀,则优秀率高的同学是________;
(3)根据图表信息,请你对这两位同学各提一条不超过20个字的学习建议.
用适当的方法解下列一元二次方程:
(1)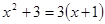 ;
;
(2)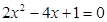 .
.