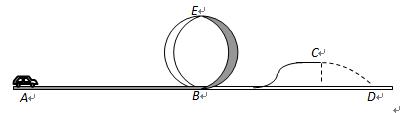
学校举行遥控赛车比赛。比赛路径如图所示,赛车从起点A出发,沿水平直线轨道运动L=10m后,由B点进入半径为R=0.4m的光滑竖直圆轨道,离开竖直圆轨道后继续沿光滑平直轨道运动,然后冲上光滑斜坡,最后从C点水平飞出落到水平轨道的D点。已知赛车质量m=0.1kg,通电后电机以额定功率P=2.0w工作了t=1.6s后关闭,此时赛车尚未到达B点。赛车到达竖直圆轨道的最高点E时对轨道的压力大小等于赛车的重力。赛车在AB段运动中所受阻力恒定。(取g=10m/s2)求:赛车在AB段运动时所受阻力的大小
同学甲认为C点离水平轨道BD越高,小车在空中飞行时间就越长,落点D离飞出点C的水平距离就越大。同学乙认为C点离水平轨道越近,小车水平飞出时的速度就越大,落点D离 飞出点C的水平距离就越大。请你通过的计算得落点D离飞出点C的最大水平位移,并对甲、乙两同学的说法做出判断。
某校一课外活动小组自制一枚火箭,设火箭发射后始终在垂直于地面的方向上运动.火箭点火后可认为做匀加速直线运动,经过4 s到达离地面40 m高处时燃料恰好用完,若不计空气阻力,取g="10" m/s2,求:
(1)燃料恰好用完时火箭的速度;
(2)火箭上升离地面的最大高度;
(3)火箭从发射到残骸落回地面过程的总时间.
在正常情况下,火车以54km/h的速度匀速开过一个小站.现因需要,必须在这一小站停留,火车将要到达小站时,以-0.5m/s2的加速度做匀减速运动,停留2分钟后,又以0.3m/s2的加速度出小站,一直到恢复原来的速度.求因列车停靠小站而延误的时间.
物体做匀加速直线运动,初速度v0=4m/s,加速度为a=2m/s2,求:
(1)物体运动的前2秒时间内的位移是多少?
(2)物体运动到第3秒初的速度是多少?
一辆执勤的警车停在公路边,当警员发现从他旁边以10m/s的速度匀速行驶的货车严重超载时,决定前去追赶,经过5.5s后警车发动起来,并以2.5m/s2的加速度做匀加速运动,但警车的行驶速度必须控制在90km/h.问:
(1)警车在追赶货车的过程中,两车间的最大距离?
(2)判定警车在加速阶段能否追上货车?
(3)警车发动后要多长时间才能追上货车?
2012年9月25日,改装后的瓦良格号航空母舰航母“辽宁号”入列,中国成为拥有航空母舰的国家之一。已知该航空母舰飞行甲板长度为L=300 m,(舰长304米)某种战斗机在航空母舰上起飞过程中的最大加速度为a=4.5 m/s2,飞机速度要达到v=60 m/s才能安全起飞。
(1)通过计算判断,飞机能否靠自身的发动机从舰上起飞?
(2)如果航空母舰静止,战斗机被弹射装置弹出后开始加速,要保证飞机起飞安全,战斗机被弹射装置弹出时的速度至少是多大?