如图所示,BC是半径为R的1/4圆弧形光滑绝缘轨道,轨道位于竖直平面内,其下端与水平绝缘轨道平滑连接,整个轨道处在水平向左的匀强电场中,电场强度为E。现有一质量为m的带电小滑块(体积很小可视为质点),在BC轨道的D点释放后可以静止不动。已知OD与竖直方向的夹角为α =37°,随后把它从C点由静止释放,滑到水平轨道上的A点时速度减为零。若已知滑块与水平轨道间的动摩擦因数为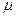 =0.25,且sin370 ="0.6 " cos370 ="0.8 " tan37°=0.75。取重力加速度为g求:
=0.25,且sin370 ="0.6 " cos370 ="0.8 " tan37°=0.75。取重力加速度为g求: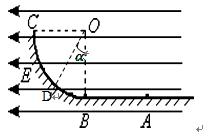
滑块的带电量q1和带电种类;
水平轨道上A、B两点之间的距离L;
滑块从C点下滑过程中对轨道的最大压力;
如图甲所示,质量分别为m、M的物体A、B静止在劲度系数为k的弹簧上,A与B不粘连。现对物体A施加竖直向上的力F,使A、B一起上升,若以两物体静止时的位置为坐标原点,两物体的加速度随位移的变化关系如图乙所示。求: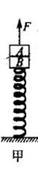
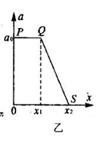
(1)当x=x1时,A、B间弹力FN;
(2)从静止开始到x=x2过程中,物体A机械能的变化量。
如图所示,在水平光滑直导轨上,静止着三个质量均为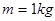 的相同小球A、B、C。现让A球以
的相同小球A、B、C。现让A球以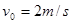 的速度向B球运动,A、B两球碰撞后粘合在一起,两球继续向右运动并跟C球碰撞,碰后C球的速度
的速度向B球运动,A、B两球碰撞后粘合在一起,两球继续向右运动并跟C球碰撞,碰后C球的速度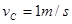 。求:
。求:
①A、B两球碰撞后瞬间的共同速度;
②两次碰撞过程中损失的总动能。
半径为R的玻璃半圆柱体,横截面如图所示,圆心为O。两条平行单色红光沿截面射向圆柱面方向与底面垂直。光线1的入射点A为圆柱面的顶点,光线 2的入射点B,∠AOB=60°,已知该玻璃对红光的折射率n=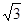 。求:
。求: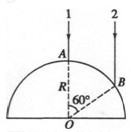
(1)两条光线经柱面和底面折射后出射光线的交点与O点的距离d;
(2)若入射的是单色蓝光,则距离d将比上面求得的结果大还是小?(定性分析,不需要计算,画出光路图)
如图所示,A、B气缸的长度均为60 cm,截面积均为40 cm2,C是可在气缸内无摩擦滑动的、体积不计的活塞,D为阀门.整个装置均由导热材料制成.原来阀门关闭,A内有压强pA = 2.4×105 Pa的氧气.B内有压强pB = 1.2×105 Pa的氢气.阀门打开后,活塞C向右移动,最后达到平衡.(假定氧气和氢气均视为理想气体,连接气缸的管道体积可忽略,环境温度不变)求: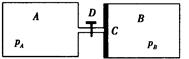
①活塞C移动的距离及平衡后B中气体的压强;
②活塞C移动过程中B中气体是吸热还是放热(简要说明理由).
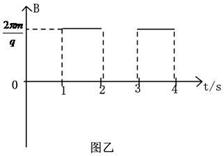
如图甲所示,水平轨道光滑,小球质量为m,带电荷量为+q,可看做质点,空间内存在不断变化的电场和磁场,磁感应强度的大小随时间的变化规律如图乙所示,磁感应强度的大小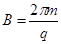 ,方向垂直纸面向里。电场在第1s、3s、5s……内方向水平向右,大小为
,方向垂直纸面向里。电场在第1s、3s、5s……内方向水平向右,大小为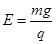 ,在第2s、4s、6s……内方向竖直向上,大小也为
,在第2s、4s、6s……内方向竖直向上,大小也为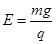 。小球从零时刻开始在A点由静止释放,求:
。小球从零时刻开始在A点由静止释放,求: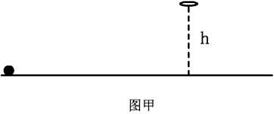
(1)t=1.5s时,小球与A点的直线距离大小;
(2)在A点前方轨道正上方高度为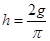 位置有一个带孔的卡片水平放置,若带电小球恰好可以从小孔中竖直穿过,求卡片与A点的水平距离大小。
位置有一个带孔的卡片水平放置,若带电小球恰好可以从小孔中竖直穿过,求卡片与A点的水平距离大小。