如图，在△ABC中，∠C=60°，BC=4，AC=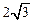
，点P在BC边上运动，PD∥AB，交AC于D. 设BP的长为x，△APD的面积为y .
（1）求AD的长（用含x的代数式表示）；
（2）求y与x之间的函数关系式，并回答当x取何值时，y的值最大？最大值是多少？
（3）点P是否存在这样的位置，使得△ADP的面积是△ABP面积的
？若存在，请求出BP的长；若不存在，请说明理由.
二次函数y=ax2+bx+c的部分对应值如下表：
| x |
… |
-2 |
-1 |
0 |
1 |
2 |
3 |
… |
| y |
… |
5 |
0 |
-3 |
-4 |
-3 |
0 |
… |
(1)二次函数图象所对应的顶点坐标为．
(2)当x=4时，y=．
(3)由二次函数的图象可知，当函数值y<0时，x的取值范围是．
如图，在Rt△OAB中，∠OAB=90°，且点B的坐标为(4，2)．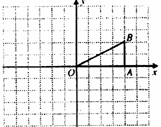
(1)画出△OAB绕点O逆时针旋转90°后的△OA1B1；
(2)求点A旋转到点A1所经过的路线长．
如图，已知CD是Rt△ABC斜边上的高，AC=4，BC=3，计算cos∠BCD的值．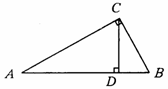
如图，已知⊙O的半径为5，弦AB=8，OC⊥AB于C，求OC的长．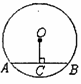
如图，OABC是一个放在平面直角坐标系中的矩形，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=3，OC=4，平行于对角线AC的直线m从原点O出发，沿x轴正方向以每秒1个单位的速度运动，设直线m与矩形OABC的两边分别交于点M、N，直线运动的时间为t(秒)．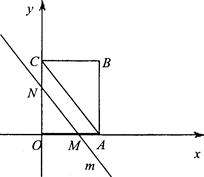
(1)写出点B的坐标；
(2)t为何值时，MN=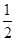
AC；
(3)设△OMN的面积为S，求S与t的函数关系式，并写出t的取值范围；当t为何值时，S有最大值?并求S的最大值．