已知f（x）=ex+x﹣2（e是自然对数的底数），则函数f（x）的导数f′（x）=（）
| A．xex﹣1﹣2x﹣3 | B．ex﹣x2 | C．ex﹣2x﹣3 | D．ex﹣x﹣2ln2 |
函数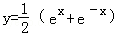
的导数是（）
A． |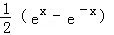
B． |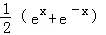
C．ex﹣e﹣x | D．ex+e﹣x |
若f（x）=sinx+cosx，则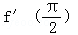
等于（）
| A．﹣1 | B．0 | C．1 | D．2 |
已知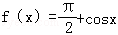
，则f′（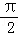
）=（）
| A．﹣1+ |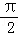
B．﹣1 | C．1 | D．0 |
设函数f（x）=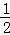
（sinx﹣cosx）的导函数为f′（x），则下列结论正确的是（）
| A．f′（x）+f（x）=﹣sinx | B．f′（x）+f（x）=﹣cosx |
| C．f′（x）﹣f（x）=sinx | D．f′（x）﹣f（x）=cosx |
B.
C.
D.