(本小题满分12分)记函数 的定义域为集合
的定义域为集合 ,函数
,函数 的定义域为集合
的定义域为集合 .
.
(1)求 ;
;
(2)若 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.
(本题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分.)
市工商局于今年3月份,对市内流通领域的饮料进行了质量监督抽查,结果显示,某种刚进入市场的 饮料的合格率为80%,现有甲,乙,丙3人聚会,选用6瓶该饮料,并限定每人喝两瓶,求
饮料的合格率为80%,现有甲,乙,丙3人聚会,选用6瓶该饮料,并限定每人喝两瓶,求
(Ⅰ)甲喝两瓶 饮料,均合格的概率
饮料,均合格的概率
(Ⅱ)甲、乙、丙每人喝两瓶,恰有一人喝到不合格饮料的概率(精确到0.01)
(本题满分13分,(Ⅰ)小问9分,(Ⅱ)小问4分.)
已知集合 ,
,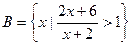 .
.
(Ⅰ)求集合 和集合
和集合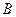
(Ⅱ)若 ,求
,求 的取值范围.
的取值范围.
某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要 维护费50元.
维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多 少?
少?
已知定义域为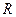 的函数
的函数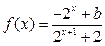 是奇函数.
是奇函数.
(1)求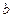 的值
的值
(2)判断函数 的单调性
的单调性
(3)若对任意的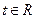 ,不等式
,不等式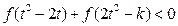 恒成立,求
恒成立,求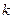
 的取值范围
的取值范围
已知函数 ,
, ,其中
,其中 ,设
,设
(1)判断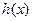 的奇偶性,并说明理由
的奇偶性,并说明理由
(2)若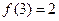 ,求使
,求使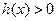 成立的x的集合
成立的x的集合